Advertisements
Advertisements
Question
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
Solution
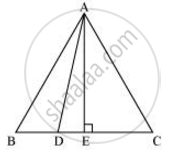
Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC.
`∴ BE = EC = (BC)/2 = a/2`
And, AE = `(asqrt3)/2`
Given that, BD = `1/3BC`
∴ BD = a/3
`DE = BE - BD = a/2 - a/3 = a/6`
Applying Pythagoras theorem in ΔADE, we get
AD2 = AE2 + DE2
`AD^2 = ((asqrt3)/2)^2 + (a/6)^2`
`= ((3a^2)/4) + (a^2/36)`
`= (28a^2)/36`
`= 7/9 AB^2`
⇒ 9 AD2 = 7 AB2
APPEARS IN
RELATED QUESTIONS
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
In the figure, find AR
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
