Advertisements
Advertisements
Question
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
Solution
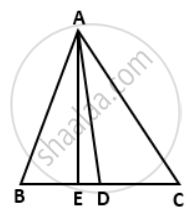
We have ∠AED = 90°
∴ ∠ADE < 90° and ∠ADC > 90°
i.e. ∠ADE is acute and ∠ADC is obtuse.
In ΔABD, ∠ADE is an acute angle.
∴ AB2 = AD2 + BD2 - 2 x BD x DE
⇒ AB2 = AD2 + `(1/2"BC")^2 - 2 xx (1)/(2)"BC" xx "DE"`
⇒ AB2 = AD2 + `(1)/(4)"BC"^2 - "BC" xx "DE"`
⇒ AB2 = AD2 + BC x DE - `(1)/(4)"BC"^2`. ....(ii)
APPEARS IN
RELATED QUESTIONS
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.
Prove that : 2AC2 = 2AB2 + BC2
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
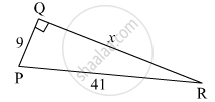
In the figure below, find the value of 'x'.
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
Find the unknown side in the following triangles
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
