Advertisements
Advertisements
प्रश्न
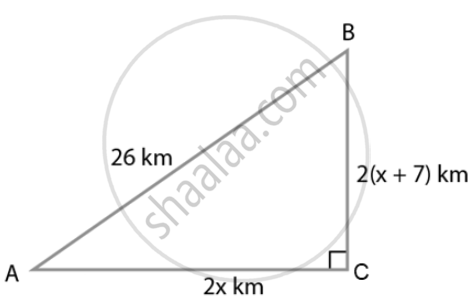
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
उत्तर
According to the question,
AC ⊥ CB,
AC = 2x km,
CB = 2(x + 7) km
And AB = 26 km
Thus, we get ∆ACB right angled at C.
Now, from ∆ACB,
Using Pythagoras Theorem,
AB2 = AC2 + BC2
⇒ (26)2 = (2x)2 + {2(x + 7)}2
⇒ 676 = 4x2 + 4(x2 + 196 + 14x)
⇒ 676 = 4x2 + 4x2 + 196 + 56x
⇒ 676 = 82 + 56x + 196
⇒ 8x2 + 56x – 480 = 0
Dividing the equation by 8, we get,
x2 + 7x – 60 = 0
x2 + 12x – 5x – 60 = 0
x(x + 12) – 5(x + 12) = 0
(x + 12)(x – 5) = 0
∴ x = –12 or x = 5
Since the distance can’t be negative, we neglect x = –12
∴ x = 5
Now,
AC = 2x = 10 km
BC = 2(x + 7)
= 2(5 + 7)
= 24 km
Thus, the distance covered to city B from city A via city C = AC + BC
AC + BC = 10 + 24
= 34 km
Distance covered to city B from city A after the highway was constructed = BA = 26 km
Therefore, the distance saved = 34 – 26 = 8 km.
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
Find the Pythagorean triplet from among the following set of numbers.
4, 5, 6
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
Find the unknown side in the following triangles
Two circles having same circumference are congruent.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
