Advertisements
Advertisements
प्रश्न
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
उत्तर
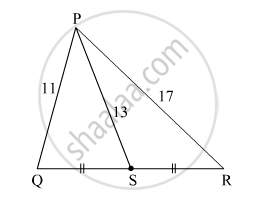
In ∆PQR, point S is the midpoint of side QR.
\[{PQ}^2 + {PR}^2 = 2 {PS}^2 + 2 {QS}^2\] .......…[Apollonius theorem]
\[ \Rightarrow {11}^2 + {17}^2 = 2 \left( 13 \right)^2 + 2 {QS}^2 \]
\[ \Rightarrow 121 + 289 = 2\left( 169 \right) + 2 {QS}^2 \]
\[ \Rightarrow 410 = 338 + 2 {QS}^2 \]
\[ \Rightarrow 2 {QS}^2 = 410 - 338\]
\[ \Rightarrow 2 {QS}^2 = 72\]
\[ \Rightarrow {QS}^2 = 36\]
\[ \Rightarrow QS = 6\]
\[ \therefore QR = 2 \times QS\]
\[ = 2 \times 6\]
\[ = 12\]
Hence, QR = 12.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 7 cm, 24 cm, 25 cm
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, ho much string does she have out (see Figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
In a right angled triangle, the hypotenuse is the greatest side
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
In a right-angled triangle ABC, if angle B = 90°, then which of the following is true?
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
