SSC (English Medium)
SSC (Marathi Semi-English)
Academic Year: 2019-2020
Date & Time: 14th March 2020, 11:00 am
Duration: 2h
Advertisements
- All questions are compulsory.
- Use of calculator is not allowed.
- The numbers to the right of the questions indicate full marks.
- In the case of MCQ’s Q. No. 1(A) only the first attempt will be evaluated and will be given credit.
- For every MCQ, the correct alternative (A), (B), (C) or (D) in front of subquestion number is to be written as an answer.
Out of the following, which is the Pythagorean triplet?
(1, 5, 10)
(3, 4, 5)
(2, 2, 2)
(5, 5, 2)
Chapter: [0.02] Pythagoras Theorem
Two circles of radii 5.5 cm and 3.3 cm respectively touch each other externally. What is the distance between their centres?
4.4 cm
2.2 cm
8.8 cm
8.9 cm
Chapter: [0.03] Circle
Fill in the blank using correct alternative.
Distance of point (–3, 4) from the origin is ______.
7
1
5
−5
Chapter: [0.05] Co-ordinate Geometry
Find the volume of a cube of side 3 cm ______.
27 cm3
9 cm3
81 cm3
3 cm3
Chapter: [0.07] Mensuration
The ratio of corresponding sides of similar triangles is 3 : 5, then find the ratio of their areas.
Chapter: [0.01] Similarity
Find the diagonal of a square whose side is 10 cm.
Chapter: [0.07] Mensuration
`square`ABCD is cyclic. If ∠B = 110°, then find measure of ∠D.
Chapter: [0.03] Circle
Find the slope of the line passing through the points A(2, 3) and B(4, 7).
Chapter: [0.05] Co-ordinate Geometry
Advertisements
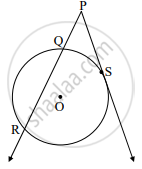
In the figure given above, ‘O’ is the centre of the circle, seg PS is a tangent segment and S is the point of contact. Line PR is a secant.
If PQ = 3.6, QR = 6.4, find PS.
Solution:
PS2 = PQ × `square` ......(tangent secant segments theorem)
= PQ × (PQ + `square`)
= 3.6 × (3.6 + 6.4)
= 3.6 × `square`
= 36
∴ PS = `square` .....(by taking square roots)
Chapter: [0.03] Circle
If sec θ = `25/7`, find the value of tan θ.
Solution:
1 + tan2 θ = sec2 θ
∴ 1 + tan2 θ = `(25/7)^square`
∴ tan2 θ = `625/49 - square`
= `(625 - 49)/49`
= `square/49`
∴ tan θ = `square/7` ........(by taking square roots)
Chapter: [0.06] Trigonometry
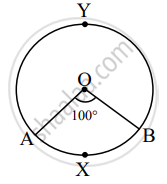
In the figure given above, O is the centre of the circle. Using given information complete the following table:
| Type of arc | Name of the arc | Measure of the arc |
| Minor arc | `square` | `square` |
| Major arc | `square` | `square` |
Chapter: [0.03] Circle
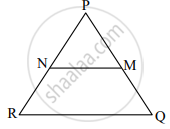
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
Chapter: [0.01] Similarity
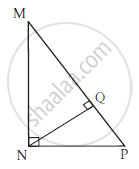
In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
Chapter: [0.02] Pythagoras Theorem
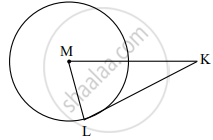
In the given figure, M is the centre of the circle and seg KL is a tangent segment. L is a point of contact. If MK = 12, KL = `6sqrt3`, then find the radius of the circle.
Chapter: [0.03] Circle
Find the coordinates of midpoint of the segment joining the points (22, 20) and (0, 16).
Chapter: [0.05] Co-ordinate Geometry
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
Chapter: [0.06] Trigonometry
Advertisements
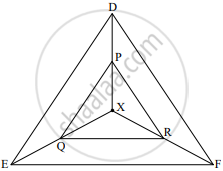
In the given figure, X is any point in the interior of the triangle. Point X is joined to the vertices of triangle. seg PQ || seg DE, seg QR || seg EF. Complete the activity and prove that seg PR || seg DF.
Proof:
In ΔXDE, PQ || DE ......(Given)
∴ `"XP"/"PD" = square/"QE"` ......(Basic proportionality theorem)…(i)
In ΔXEF, QR || EF ......(Given)
∴ `"XQ"/square = "XR"/square` ..........(`square`)....(ii)
∴ `"XP"/"PD" = square/square` ......[From (i) and (ii)]
∴ seg PR || seg DF ......(By converse of basic proportionality theorem
Chapter: [0.01] Similarity
If A(6, 1), B(8, 2), C(9, 4) and D(7, 3) are the vertices of `square`ABCD, show that `square`ABCD is a parallelogram.
Solution:
Slope of line = `("y"_2 - "y"_1)/("x"_2 - "x"_1)`
∴ Slope of line AB = `(2 - 1)/(8 - 6) = square` .......(i)
∴ Slope of line BC = `(4 - 2)/(9 - 8) = square` .....(ii)
∴ Slope of line CD = `(3 - 4)/(7 - 9) = square` .....(iii)
∴ Slope of line DA = `(3 - 1)/(7 - 6) = square` .....(iv)
∴ Slope of line AB = `square` ......[From (i) and (iii)]
∴ line AB || line CD
∴ Slope of line BC = `square` ......[From (ii) and (iv)]
∴ line BC || line DA
Both the pairs of opposite sides of the quadrilateral are parallel.
∴ `square`ABCD is a parallelogram.
Chapter: [0.05] Co-ordinate Geometry
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
Chapter: [0.02] Pythagoras Theorem
Prove the following theorem:
Tangent segments drawn from an external point to the circle are congruent.
Chapter: [0.03] Circle
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Chapter: [0.04] Geometric Constructions
A metal cuboid of measures 16 cm × 11 cm × 10 cm was melted to make coins. How many coins were made, if the thickness and diameter of each coin was 2 mm and 2 cm respectively? (π = 3.14)
Chapter: [0.07] Mensuration
In ΔABC, PQ is a line segment intersecting AB at P and AC at Q such that seg PQ || seg BC. If PQ divides ΔABC into two equal parts having equal areas, find `"BP"/"AB"`.
Chapter: [0.01] Similarity
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
Chapter: [0.03] Circle
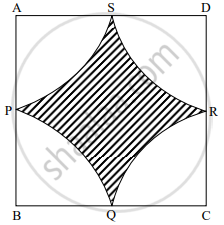
In the given figure `square`ABCD is a square of side 50 m. Points P, Q, R, S are midpoints of side AB, side BC, side CD, side AD respectively. Find area of shaded region
Chapter: [0.07] Mensuration
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
Chapter: [0.03] Circle
If sin θ + sin2 θ = 1 show that: cos2 θ + cos4 θ = 1
Chapter: [0.06] Trigonometry
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 10th Standard Board Exam Geometry Mathematics 2 with solutions 2019 - 2020
Previous year Question paper for Maharashtra State Board 10th Standard Board Exam Geometry Maths 2-2020 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Geometry Mathematics 2, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 10th Standard Board Exam.
How Maharashtra State Board 10th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Geometry Mathematics 2 will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
