Advertisements
Advertisements
प्रश्न
A metal cuboid of measures 16 cm × 11 cm × 10 cm was melted to make coins. How many coins were made, if the thickness and diameter of each coin was 2 mm and 2 cm respectively? (π = 3.14)
उत्तर
Volume of cuboid = l × b × h
= 16 × 11 × 10
= 1760 cm3
Thickness of coin (H) = 2 mm
= 0.2 cm ...[∵ 1 cm = 10 mm]
Diameter of coin (D) = 2 cm
∴ Radius of coin (R) = `"D"/2 = 2/2` = 1 cm
∴ Volume of one coin = πR2H
= `3.14 xx 1^2 xx 0.2`
= 0.629 cm3
Number of coins that were made = `"Volume of cuboid"/"Volume of one coin"`
= `1760/0.629`
= 2800
∴ 2800 coins were made by melting the cuboid.
APPEARS IN
संबंधित प्रश्न
Due to heavy floods in a state, thousands were rendered homeless. 50 schools collectively offered to the state government to provide place and the canvas for 1500 tents to be fixed by the governments and decided to share the whole expenditure equally. The lower part of each tent is cylindrical of base radius 2.8 cm and height 3.5 m, with conical upper part of same base radius but of height 2.1 m. If the canvas used to make the tents costs Rs. 120 per sq. m, find the amount shared by each school to set up the tents. What value is generated by the above problem? (use `pi =22/7`)
In a rain-water harvesting system, the rain-water from a roof of 22 m × 20 m drains into a cylindrical tank having diameter of base 2 m and height 3·5 m. If the tank is full, find the rainfall in cm. Write your views on water conservation.
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of canvas required for the tent.
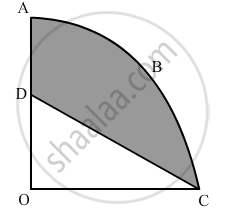
In Figure 3, OABC is a quadrant of a circle of radius 7 cm. If OD = 4 cm, find the area of the shaded region ?\[[Use\pi = \frac{22}{7}]\]
Find the total surface area of a cylinder if the radius of its base is 5 cm and height is 40 cm.
The capacity of a certain cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its height and length are 10 m and 2.5 m respectively.
Water flows through a cylindrical pipe , whose inner radius is 1 cm , at the rate of 80 cm /sec in an empty cylindrical tank , the radius of whose base is 40 cm . What is the rise of water level in tank in half an hour ?
A building is in the form of a cylinder surrounded by a hemispherical dome. The base diameter of the dome is equal to \[\frac{2}{3}\] of the total height of the building . Find the height of the building , if it contains \[67\frac{1}{21} m^3\].
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cubic cm of iron weighs 7.5 gm.
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water . Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm .
The surface area of a sphere is 616 cm2 . Find its radius.
No Question.
If each edge of a cube is increased by 50%, the percentage increase in the surface area is
The diameter of the base of a cylinder is 4 cm and its height is 14 cm. The volume of the cylinder is
The area of the base of a right circular cone is 154 cm2 and its height is 14 cm. Its curved surface area is
If the radii of the ends of a bucket are 5 cm and 15 cm and it is 24 cm high, then its surface area is
The slant height of the frustum of a cone is 4 cm and the perimeters (i.e. circumferences) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Arrange the given objects according to their volume
A running track has 2 semicircular ends of radius 63 m and two straight lengths. The perimeter of the track is 1000 m. Find each straight length.
