Advertisements
Advertisements
प्रश्न
Find the total surface area of a cylinder if the radius of its base is 5 cm and height is 40 cm.
उत्तर
Radius of the cylinder, r = 5 cm
Height of the cylinder, h = 40 cm
∴ Total surface area of cylinder, S = \[2 π r\left( r + h \right) = 2 \times 3 . 14 \times 5 \times \left( 5 + 40 \right) = 2 \times 3 . 14 \times 5 \times 45\] = 1413 cm2
Thus, the total surface area of cylinder is 1413 cm2.
APPEARS IN
संबंधित प्रश्न
Water is flowing at the rate of 2.52 km/h through a cylindrical pipe into a cylindrical tank, the radius of whose base is 40 cm. If the increase in the level of water in the tank, in half an hour is 3.15 m, find the internal diameter of the pipe.
Sushant has a vessel, of the form of an inverted cone, open at the top, of height 11 cm and radius of top as 2.5 cm and is full of water. Metallic spherical balls each of diameter 0.5 cm are put in the vessel due to which 2/5 th of the water in the vessel flows out. Find how many balls were put in the vessel. Sushant made the arrangement so that the water that flows out irrigates the flower beds. What value has been shown by Sushant?
To fill a swimming pool two pipes are to be used. If the pipe of larger diameter is used for 4 hours and the pipe of smaller diameter for 9 hours, only half the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool.
A right triangle whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate.)
Water is flowing through a cylindrical pipe, of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m/s. Determine the rise in level of water in the tank in half an hour ?
Find the ratio of the volumes of a cylinder and a cone having equal radius and equal height.
(A)1 : 2 (B) 2 : 1 (C) 1 : 3 (D) 3 : 1
The capacity of a certain cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its height and length are 10 m and 2.5 m respectively.
What is the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height?
A sphere of radius 6 cm is dropped into a cylindrical vessel partly filled with water. The radius of the vessel is 8 cm. If the sphere is submerged completely, then the surface of the water rises by
The curved surface area of a cylinder is 264 m2 and its volume is 924 m3. The ratio of its diameter to its height is
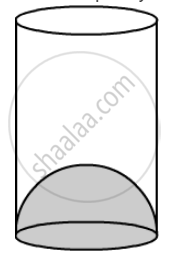
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure. If the height of the glass is 16 cm, find the apparent capacity and the actual capacity of the glass.
Water is flowing at the rate of 6 km/hr through a pipe of diameter 14 cm into a rectangular tank which is 60 m long and 22 m wide. Determine the time in which the level of water in the tank will rise by 7 cm.
A solid cone of base radius 10 cm is cut into two parts through the midpoint of its height, by a plane parallel to its base. Find the ratio of the volumes of the two parts of the cone.
Choose the correct answer of the following question:
The surface areas of two spheres are in the ratio 16 : 9. The ratio of their volumes is
The ratio between the radius of the base and the height of a cylinder is 2 : 3. If its volume is 1617 cm3, the total surface area of the cylinder is
Two cubes, each of volume 64 cm3, are joined end to end. Find the total surface area of the resulting cuboid.

In the above figure, a sphere is placed in a cylinder. It touches the top, bottom and curved surface of the cylinder. If the radius of the base of the cylinder is ‘r’, write the answer to the following questions.
a. What is the height of the cylinder in terms of ‘r’?
b. What is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
c. What is the ratio of volumes of the cylinder and of the sphere?
The slant height of a bucket is 26 cm. The diameter of upper and lower circular ends are 36 cm and 16 cm. then height of bucket is ______.
The capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom as shown in the figure is `(pir^2)/3 [3h - 2r]`.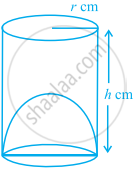
A running track has 2 semicircular ends of radius 63 m and two straight lengths. The perimeter of the track is 1000 m. Find each straight length.
