Advertisements
Advertisements
प्रश्न
Sushant has a vessel, of the form of an inverted cone, open at the top, of height 11 cm and radius of top as 2.5 cm and is full of water. Metallic spherical balls each of diameter 0.5 cm are put in the vessel due to which 2/5 th of the water in the vessel flows out. Find how many balls were put in the vessel. Sushant made the arrangement so that the water that flows out irrigates the flower beds. What value has been shown by Sushant?
उत्तर
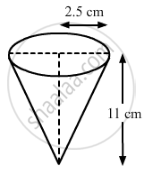
Height (h) of the conical vessel = 11 cm
Radius (r1) of the conical vessel = 2.5 cm
Radius (r2) of the metallic spherical balls =0.5/2 =0.25 cm
Let n be the number of spherical balls that were dropped in the vessel.
Volume of the water spilled = Volume of the spherical balls dropped
`2/5xx"Volume of cone" = nxx"Volume of one spherical ball"`
`⇒2/5xx1/3πr_1^2h = nxx4/3πr_2^3`
`⇒r_1^2h=nxx10r_2^3`
`⇒(2.5)^2×11=n×10×(0.25)^3`
`⇒68.75=0.15625n`
`⇒n=440`
Hence, the number of spherical balls that were dropped in the vessel is 440.
Sushant made the arrangement so that the water that flows out, irrigates the flower beds. This shows the judicious usage of water.
APPEARS IN
संबंधित प्रश्न
In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 7280 km2, show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
Some plastic balls of radius 1 cm were melted and cast into a tube. The thickness, length and outer radius of the tube were 2 cm, 90 cm, and 30 cm respectively. How many balls were melted to make the tube?
Radius of a sphere is 14 cm. Find the surface area of the sphere.
A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/hr. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired ?
A factory manufactures 120,000 pencils daily . The pencil are cylindrical in shape each of length 25 cm and circumference of base as 1.5 cm . Determine the cost of colouring the curved surfaces of the pencils manufactured in one day at ₹0.05 per dm2.
The radii of the ends of a bucket of height 24 cm are 15 cm and 5 cm. Find its capacity. (Take π = 22/7)
The length of the longest pole that can be kept in a room (12 m × 9 m ×8 m) is
The curved surface area of a cylindrical pillar is 264 m2 and its volume is 924 m3. The height of the pillar is
A right circular cylinder of radius r cm and height h cm (h > 2r) just encloses a sphere of diameter ______.
The curved surface area of a right circular cone is 12320 cm2. If the radius of its base is 56 cm, then find its height.
