Advertisements
Advertisements
Question
Sushant has a vessel, of the form of an inverted cone, open at the top, of height 11 cm and radius of top as 2.5 cm and is full of water. Metallic spherical balls each of diameter 0.5 cm are put in the vessel due to which 2/5 th of the water in the vessel flows out. Find how many balls were put in the vessel. Sushant made the arrangement so that the water that flows out irrigates the flower beds. What value has been shown by Sushant?
Solution
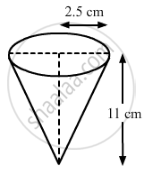
Height (h) of the conical vessel = 11 cm
Radius (r1) of the conical vessel = 2.5 cm
Radius (r2) of the metallic spherical balls =0.5/2 =0.25 cm
Let n be the number of spherical balls that were dropped in the vessel.
Volume of the water spilled = Volume of the spherical balls dropped
`2/5xx"Volume of cone" = nxx"Volume of one spherical ball"`
`⇒2/5xx1/3πr_1^2h = nxx4/3πr_2^3`
`⇒r_1^2h=nxx10r_2^3`
`⇒(2.5)^2×11=n×10×(0.25)^3`
`⇒68.75=0.15625n`
`⇒n=440`
Hence, the number of spherical balls that were dropped in the vessel is 440.
Sushant made the arrangement so that the water that flows out, irrigates the flower beds. This shows the judicious usage of water.
APPEARS IN
RELATED QUESTIONS
To fill a swimming pool two pipes are to be used. If the pipe of larger diameter is used for 4 hours and the pipe of smaller diameter for 9 hours, only half the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool.
A hemispherical bowl of internal radius 9 cm is full of water. Its contents are emptied in a cylindrical vessel of internal radius 6 cm. Find the height of water in the cylindrical vessel.
Find the total surface area of a cylinder if the radius of its base is 5 cm and height is 40 cm.
A building is in the form of a cylinder surmounted by a hemi-spherical vaulted dome and contains \[41\frac{19}{21} m^3\] of air. If the internal diameter of dome is equal to its total height above the floor , find the height of the building ?
A conical vessel whose internal radius is 10 cm and height 48 cm is full of water. Find the volume of water. If this water is poured into a cylindrical vessel with internal radius 20 cm, find the height to which the water level rises in it.
Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m × 16 m × 11 m.
A hemispherical tank full of water is emptied by a pipe at the rate of \[\frac{25}{7}\] litres per second. How much time will it take to half-empty the tank, If the tank is 3 metres in diameter?
If the volumes of two cones are in the ratio 1 : 4 and their diameters are in the ratio 4 : 5, then write the ratio of their weights.
The surface areas of the six faces of a rectangular solid are 16, 16, 32, 32, 72 and 72 square centimetres. The volume of the solid, in cubic centimetres, is ______.
The radius of a metal sphere is 3 cm. The sphere is melted and made into a long wire of uniform circular cross-section, whose length is 36 cm. To calculate the radius of wire, complete the following activity.
Radius of the sphere = `square`
Length of the wire = `square`
Let the radius of the wire by r cm.
Now, Volume of the wire = Volume of the `square`
`square` = `square`
r2 × `square` = `square` × `square`
r2 × `square` = `square`
r = `square`
Hence, the radius of the wire is `square` cm.
