Advertisements
Advertisements
प्रश्न
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
उत्तर
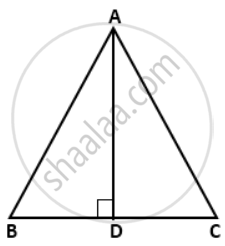
Since triangle ABD and ACD are right triangle right-angled at D,
AB2 = AD2 + BD2 ....(i)
AC2 = AD2 + CD2 ....(ii)
Subtracting (ii) and (i), we get
AB2 - AC2 = BD2 - CD2
⇒ AB2 + CD2 = AC2 + BD2.
APPEARS IN
संबंधित प्रश्न
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
In the right-angled ∆PQR, ∠ P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
Find the length of the support cable required to support the tower with the floor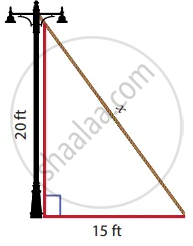
In an equilateral triangle PQR, prove that PS2 = 3(QS)2.

Two angles are said to be ______, if they have equal measures.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
