Advertisements
Advertisements
प्रश्न
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
उत्तर
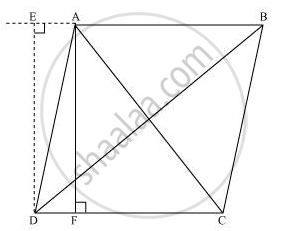
Let ABCD be a parallelogram.
Let us draw perpendicular DE on extended side AB, and AF on side DC.
Applying Pythagoras theorem in ΔDEA, we obtain
DE2 + EA2 = DA2 … (i)
Applying Pythagoras theorem in ΔDEB, we obtain
DE2 + EB2 = DB2
DE2 + (EA + AB)2 = DB2
(DE2 + EA2) + AB2 + 2EA × AB = DB2
DA2 + AB2 + 2EA × AB = DB2 … (ii)
Applying Pythagoras theorem in ΔADF, we obtain
AD2 = AF2 + FD2
Applying Pythagoras theorem in ΔAFC, we obtain
AC2 = AF2 + FC2
= AF2 + (DC − FD)2
= AF2 + DC2 + FD2 − 2DC × FD
= (AF2 + FD2) + DC2 − 2DC × FD
AC2 = AD2 + DC2 − 2DC × FD … (iii)
Since ABCD is a parallelogram,
AB = CD … (iv)
And, BC = AD … (v)
In ΔDEA and ΔADF,
∠DEA = ∠AFD (Both 90°)
∠EAD = ∠ADF (EA || DF)
AD = AD (Common)
∴ ΔEAD `~=` ΔFDA (AAS congruence criterion)
⇒ EA = DF … (vi)
Adding equations (i) and (iii), we obtain
DA2 + AB2 + 2EA × AB + AD2 + DC2 − 2DC × FD = DB2 + AC2
DA2 + AB2 + AD2 + DC2 + 2EA × AB − 2DC × FD = DB2 + AC2
BC2 + AB2 + AD2 + DC2 + 2EA × AB − 2AB × EA = DB2 + AC2
[Using equations (iv) and (vi)]
AB2 + BC2 + CD2 + DA2 = AC2 + BD2
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
Side of a triangle is given, determine it is a right triangle.
`(2a – 1) cm, 2\sqrt { 2a } cm, and (2a + 1) cm`
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
Find the unknown side in the following triangles
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
