Advertisements
Advertisements
Question
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution
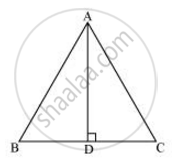
Let AD be the altitude in the given equilateral triangle, ΔABC.
We know that altitude bisects the opposite side.
∴ BD = DC = a
In ΔADB
∠ADB = 90º
Applying pythagoras theorem we obtain
AD2 + DB2 = AD2
⇒ AD2 + a2 = (2a)2
⇒ AD2 + a2 = 4a2
⇒ AD2 = 3a2
⇒ AD =`asqrt3`
In an equilateral triangle, all the altitudes are equal in length. Therefore, the length of each altitude will be `sqrt3a`
APPEARS IN
RELATED QUESTIONS
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
Find the length of diagonal of the square whose side is 8 cm.
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
