Advertisements
Advertisements
Question
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
Solution
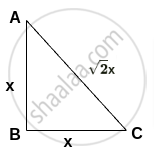
Let, the sides of the triangle be, x: `sqrt2`x and x.
AB2 + BC2 = x2 +x2 = 2x2
AC2 = `(sqrt2 x)^2` = 2x2
AB2 + BC2 = AC2
Conversely, if in any triangle, the square on the largest side of the triangle is equal to the sum of the squares on remaining two sides, then the triangle is a right-angled triangle and the angle opposite to the largest side is a right-angle.
Therefore, Δ ABC is a right-angled triangle.
APPEARS IN
RELATED QUESTIONS
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of `(20 "km")/"hr"` and the second train travels at `(30 "km")/"hr"`. After 2 hours, what is the distance between them?
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
