Advertisements
Advertisements
प्रश्न
A vessel in the form of an inverted cone is filled with water to the brim: Its height is 20 cm and the diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cones submerged?
उत्तर
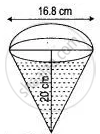
Height = 20 cm, diameter = 16.8 cm or radius = `16.8/2` = 8.4 cm.
Volume of water in bigger cone = `1/3`πr2h
= `1/3 xx 22/7` x 8.4 x 8.4 x 20
= 1478.4 cm3
Volume of water overflows when two equal cone is submerged = `1/3` x 1478.4
= 492.8 cm3
∴ Volume of two equal cones = 492.8
So volume of each cone = `1/2` x 492.8 = 246.4 cm3.
APPEARS IN
संबंधित प्रश्न
Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Find the ratio of the curved surface areas of two cones if their diameters of the bases are equal and slant heights are in the ratio 4 : 3.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs. 210 per l00 m2.
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 2 m canvas is Rs. 70, find the cost of the canvas required to make the tent.
The circumference of the base of a 10 m height conical tent is 44 metres. Calculate the length of canvas used in making the tent if width of canvas is 2 m. (Use it 𝜋= 22/7).
The radius and height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the slant height and radius of the cone. (Use it 𝜋 = 3.14).
A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm.
The diameter of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surface areas.
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. Find the radius of the base of each smaller cone, if height of each is 108 cm
A solid metallic hemisphere of diameter 28 cm is melted and recast into a number of identical solid cones, each of diameter 14 cm and height 8 cm. Find the number of cones so formed.
A cone and a hemisphere have the same base and the same height. Find the ratio between their volumes.
Volume of a cone is 1232 cm3 and its height is 24 cm. Find the surface area of the cone. `( π = 22/7)`
The radius and height of a cylinder, a cone and a sphere are same. Calculate the ratio of their volumes.
A buoy is made in the form of a hemisphere surmounted by a right circular cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 m and its volume is two-third the volume of hemisphere. Calculate the height of the cone and the surface area of the buoy, correct to two decimal places.
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown. Calculate: the density of the material if its total weight is 1.7 kg
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
