Advertisements
Advertisements
प्रश्न
A metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3.5 m. Calculate: the total area of the internal surface, excluding the base.
उत्तर
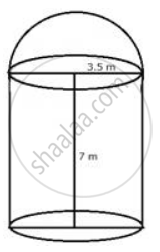
Radius of the cylinder = 3.5 m
Height = 7 m
Total surface area of container excluding the base = Curved
surface area of the cylinder + area of hemisphere
`= 2 pi"rh" + 2pi "r"^2`
`= (2xx22/7 xx 3.5 xx 7) + (2 xx 22/7 xx 3.5 xx 3.5)`
= 154 + 77 m2
= 231 m2
APPEARS IN
संबंधित प्रश्न
The circumference of the base of the cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1000 cm3 = 1l)
`["Assume "pi=22/7]`
A hollow cylinder has solid hemisphere inward at one end and on the other end it is closed with a flat circular plate. The height of water is 10 cm when flat circular surface is downward. Find the level of water, when it is inverted upside down, common diameter is 7 cm and height of the
cylinder is 20 cm.
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for `4 1/2` seconds at the rate of 9 complete rounds per second. Find the area covered by the cylinder in `4 1/2` seconds.
A closed cylindrical tank, made of thin ironsheet, has diameter = 8.4 m and height 5.4 m. How much metal sheet, to the nearest m2, is used in making this tank, if `1/15` of the sheet actually used was wasted in making the tank?
Water flows through a cylindrical pipe of internal diameter 7 cm at 36 km/hr. Calculate the time in minutes it would take to fill the cylindrical tank, the radius of whose base is 35 cm, and height is 1 m.
A rectangular paper of width 14 cm is rolled along its width and a cylinder of radius 20 cm is formed. Find the volume of the cylinder. (Take `22/7` for π)

A right-angled triangle whose sides are 6 cm, 8 cm and 10 cm is revolved about the sides containing the right angle in two ways. Find the difference in volumes of the two solids so formed.
Find the number of coins, 1.5 cm in diameter and 2 mm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm
Radius of a cylinder is r and the height is h. Find the change in the volume if the height is doubled.
Metallic discs of radius 0.75 cm and thickness 0.2 cm are melted to obtain 508.68 cm3 of metal. Find the number of discs melted (use π = 3.14).
