Advertisements
Advertisements
प्रश्न
In the adjoining figure, the crescent is formed by two circles which touch at the point A. O is the centre of bigger circle. If CB = 9 cm and DE = 5 cm, find the area of the shaded portion.
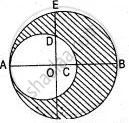
उत्तर
Let R and r be the radii of two circles. Then, 2(R - r) = 9.
Join AD and CD,
ΔAOB ∼ ΔDOC
∴ `"OD"/"OC" = "OA"/"OD"`
⇒ OD2 = OA.OC
⇒ (R - 5)2 = R(R - 9)
⇒ R2 + 25 - 10R = R2 - 9R
∴ R = 25
So, 2(25 - r) = 9
∴ r = 20.5 cm
Area of the shaded portion = πR2 - πr2
= π[ (25)2 - (20.5)2 ] cm2
= `22/7` [ 625 - 420.25 ] cm2
= `22/7` x 204.75 cm2
= 643.5 cm2.
APPEARS IN
संबंधित प्रश्न
A race track is in the form of a ring whose inner circumference is 352 m, and the outer circumference is 396 m. Find the width of the track.
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150º. Find the length of its arc and area.
The perimeter of a sector of a circle of radius 5.2 cm is 16.4 cm. Find the area of the sector.
The minute hand of a clock is 10cm long. Find the area of the face of the clock described by the minute hand between 9 A.M. and 9.35 A.M.
An elastic belt is placed round the rim of a pulley of radius 5 cm. One point on the belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from O. Find the length
of the belt that is in contact with the rim of the pulley. Also, find the shaded area.
A steel wire when bent is the form of square encloses an area of 12 cm2. If the same wire is bent in form of circle. Find the area of circle.
Find the area of the rhombus, the length of whose diagonals are 30 cm and 16 cm. Also, find the perimeter of the rhombus.
The difference between the circumference and radius of a circle is 37cm. Using `pi = 22/7` , find the circumference of the circle.
The area of a circle is 38.5 cm2. The circumference of the circle is
The perimeter of a circular field is 242 m. The area of the field is
Find the area and perimeter of the circle with the following :
Radius= 10.5 cm
The circumference of a garden roller is 280 cm. How many revolutions does it make in moving 490 meters?
A wire when bent in the form of a square encloses an area of 484 cm2. If the same wire is bent into the form of a circle, find the area of the circle.
Find the diameter of the sphere for the following :
Volume = `72pi "cm"^3`
Find the diameter of the sphere for the following :
Surface Area = 221. 76 cm2
The radius of a circle is 5 m. Find the circumference of the circle whose area is 49 times the area of the given circle.
Find the area and perimeter of the following semicircles: Diameter = 7cm
The speed of a car is 66km per hour. If each wheel of the car is 140cm in diameter, find the number if revolution made by each wheel per minute.
Sudhanshu divides a circular disc of radius 7 cm in two equal parts. What is the perimeter of each semicircular shape disc? (Use π = `22/7`)
The area of a semicircle of radius 4r is ______.
