Advertisements
Advertisements
प्रश्न
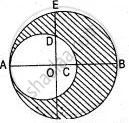
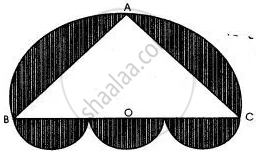
In the adjoining figure, the crescent is formed by two circles which touch at the point A. O is the centre of bigger circle. If CB = 9 cm and DE = 5 cm, find the area of the shaded portion.
उत्तर
Let R and r be the radii of two circles. Then, 2(R - r) = 9.
Join AD and CD,
ΔAOB ∼ ΔDOC
∴ `"OD"/"OC" = "OA"/"OD"`
⇒ OD2 = OA.OC
⇒ (R - 5)2 = R(R - 9)
⇒ R2 + 25 - 10R = R2 - 9R
∴ R = 25
So, 2(25 - r) = 9
∴ r = 20.5 cm
Area of the shaded portion = πR2 - πr2
= π[ (25)2 - (20.5)2 ] cm2
= `22/7` [ 625 - 420.25 ] cm2
= `22/7` x 204.75 cm2
= 643.5 cm2.
APPEARS IN
संबंधित प्रश्न
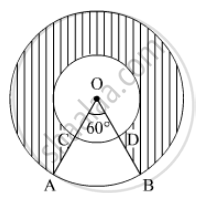
In Figure , two concentric circles with centre O, have radii 21cm and 42 cm. If ∠ AOB = 60°, find the area of the shaded region. [use π=22/7]
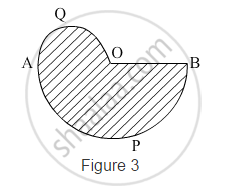
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
If the perimeter of a semi-circular protractor is 66 cm, find the diameter of the protractor (Take π = 22/7).
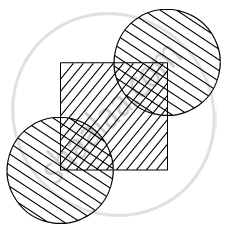
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
A doorway is decorated as shown in the figure. There are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semicircles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC, find the area of the shaded region. (Take `pi = 22/7`)
Find in terms of x the length of the arc that subtends an angle of 30°, at the centre of circle of radius 4 cm.
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Circumference of the circle
The radius of a sector of a circle is 7 cm. If the measure of the arc of the sector is 210°, find the area of the sector in case.
The difference between the circumference and radius of a circle is 37 cm. The area of the circle is
The circumference of a circle is equal to the sum of the circumference of two circles having diameters 36 cm and 20 cm. The radius of the new circle is
Sand from a cylindrical bucket 32 cm in height and 18 cm in radius is poured onto the ground making a conical heap 24 cm high. Find the radius of the conical heap.
The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has a circumference equal to the sum of circumferences of these two circles.
The radii of two circles are 48 cm and 13 cm. Find the area of the circle which has its circumference equal to the difference of the circumferences of the given two circles.
The circumference of a given circular park is 55 m. It is surrounded by a path of uniform width of 3.5 m. Find the area of the path.
The center O of a circle of a radius 1.3 cm is at a distance of 3.8 cm from a given straight line AB. Draw a circle to touch the given straight line AB at a point P so that OP = 4.7 cm and to touch the given circle externally.
If the circumference of a circle is 176 cm, find its radius.
The diameter of the wheel of a cart is 1.05 m. How much distance will the cart cover in 1000 rotations of the wheel?
The radius of the wheel of a bus is 0.7 m. How many rotations will a wheel complete while traveling a distance of 22 km?
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 28 mm
A photograph of Billiard/Snooker table has dimensions as `1/10`th of its actual size as shown in the given figure:
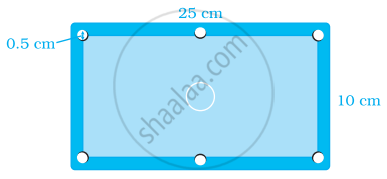
The portion excluding six holes each of diameter 0.5 cm needs to be polished at rate of ₹ 200 per m2. Find the cost of polishing.
