Advertisements
Advertisements
प्रश्न
The radii of two circles are 48 cm and 13 cm. Find the area of the circle which has its circumference equal to the difference of the circumferences of the given two circles.
उत्तर
Circumference of the first circle
s1 = 2π x 48
= 96πcm
Circumference of the first circle
s2 = 2π x 13
= 26πcm
Let r be the radius of the resulting circle.
2πr = 96π - 26π
2πr = 70π
r = `(70π)/(2π)`
= 35cm
Hence area of the circle
A = πr2
= π x 352
= 3850cm2
APPEARS IN
संबंधित प्रश्न
In Fig. there are shown sectors of two concentric circles of radii 7 cm and 3.5 cm. Find the area of the shaded region. Use π = `(\frac { 22 }{ 7 }).`
An arc of a circle is of length 5π cm and the sector it bounds has an area of 20 π cm2. Find the radius of the circle.
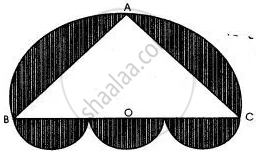
A doorway is decorated as shown in the figure. There are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semicircles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC, find the area of the shaded region. (Take `pi = 22/7`)
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
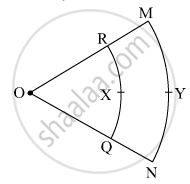
In the given figure, O is the centre of the sector. \[\angle\]ROQ = \[\angle\]MON = 60° . OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (\[\pi = \frac{22}{7}\])
Four equal circles, each of radius a units, touch each other. Show that the area between them is `(6/7"a"^2)` sq units.
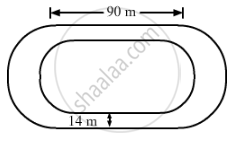
The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.
The circumference of a circle is equal to the sum of the circumference of two circles having diameters 36 cm and 20 cm. The radius of the new circle is
The areas of two circles are in the ratio 9 : 4. The ratio of their circumferences is
Sudhanshu divides a circular disc of radius 7 cm in two equal parts. What is the perimeter of each semicircular shape disc? (Use π = `22/7`)
