Advertisements
Advertisements
प्रश्न
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
उत्तर
Let the area of the resulting circle be r.
π x (16)2 + π x ( 12 )2 = π x r2
256 π + 144 π = π x r2
400π = π x r2
r2 = 400
r = 20 cm
Hence the radius of the resulting circle is 20cm.
APPEARS IN
संबंधित प्रश्न
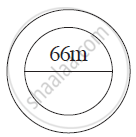
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
The cost of harvesting a square field at ₹ 900 per hectare is ₹ 8100. Find the cost of putting a fence around it at ₹ 18 per meter.
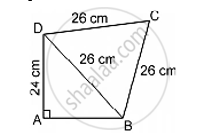
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

On increasing the diameter of a circle by 40%, its area will be increased by
Find the area of a ring-shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.
The radii of two circles are in the ratio 5 : 8. If the difference between their areas is 156p cm2, find the area of the bigger circle.
The area of the circular ring enclosed between two concentric circles is 88 cm2. Find the radii of the two circles, if their difference is 1 cm.
