Advertisements
Advertisements
प्रश्न
The radii of two circles are in the ratio 5 : 8. If the difference between their areas is 156p cm2, find the area of the bigger circle.
उत्तर
Let r1 and r2 be the radii of two circles.
⇒ r1 : r2 = 5:8
⇒`"r"_1/"r"_2 = (5)/(8)`
⇒ r1 = `(5)/(8)"r"_2`
It is given that,
πr22 - πr12 = 156π
⇒ r22 - r12 = 156
⇒ `"r"_2^2 - (5/8"r"_1)^2` = 156
⇒ `"r"_2^2 - (25)/(64)"r"_2^2` = 156
⇒ `(64"r"_2^2 - 25"r"_2^2)/(64)` = 156
⇒ 39r22 = 64 x 156
⇒ r22 = `(64 xx 156)/(39)` = 256
⇒ r2 = 16
∴ Area of bigger circle
= πr22
= `(22)/(7) xx 16 xx 16`
= 804.57cm2.
APPEARS IN
संबंधित प्रश्न
A 36-m-long, 15-m-borad verandah is to be paved with stones, each measuring 6dm by 5 dm. How many stones will be required?
The diameter of a coin is 1 cm (in the following figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).
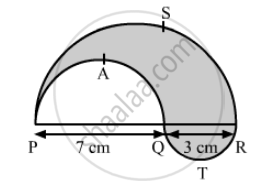
In the the following figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.
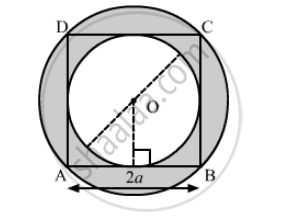
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
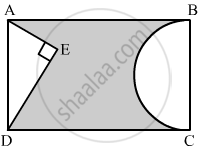
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
On decreasing the radius of a circle by 30%, its area is decreased by
In the given figure, an equilateral triangle has been inscribed in a circle of radius 4 cm. Find the area of the shaded region.

Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
