Advertisements
Advertisements
प्रश्न
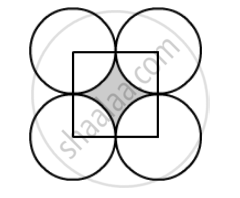
The diameter of a coin is 1 cm (in the following figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).
उत्तर
Look at the figure carefully shaded region is bounded between four sectors of the circle with same radius and a square of side 1 cm.
Therefore, the area of the shaded region is nothing but the difference the area of the square and area of one circle.
`"∴ Area of the shaded region=Area of square-Area of a circle"`
`"∴ Area of the shaded region"=1^2-pi (0.5^2)`
`"∴ Area of the shaded region"=1-0.25pi`
Substituting `pi=3.1416` we get,
`"∴ Area of the shaded region"=1-3.1416xx0.25`
`"∴ Area of the shaded region"=1-0.7854`
`"∴ Area of the shaded region"=0.2146`
Therefore, area of the shaded region is `0.2146cm^2`
APPEARS IN
संबंधित प्रश्न
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
In Figure 5, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR =12 cm. Find the lengths of QM, RN and PL ?

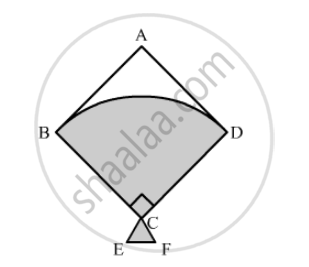
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
On increasing the diameter of a circle by 40%, its area will be increased by
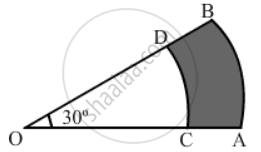
In the given figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.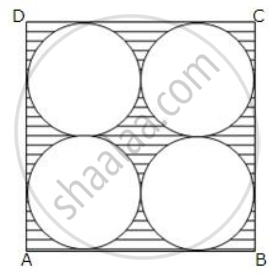
Find the area of the remaining card-board.
Find the area of a flat circular ring formed by two concentric circles (circles with the same centre) whose radii are 9 cm and 5 cm.
If the radii of two circles are in the ratio of 4 : 3, then their areas are in the ratio of ______.
