Advertisements
Advertisements
प्रश्न
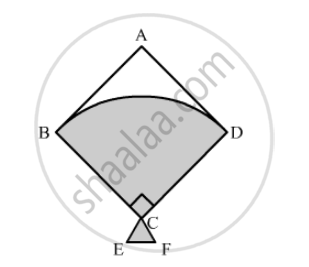
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
उत्तर
We will find the area of the shaded region as shown below,
Area of the shaded region = area of quadrant + area of isosceles triangle ……..(1)
`∴" Area of shaded region"=90/360xxpixx42^2+1/2xx6xx6`
`∴" Area of shaded region"=1/4xxpixx42^2+1/2xx36`
Substituting `pi=22/7` we get,
`∴ "Area of shaded region"=1/4xx22/7xx42^2+1/2xx36`
`∴ "Area of shaded region"=1/2xx11xx6xx42+18`
`∴ "Area of shaded region"=11xx3xx42+18`
`∴ "Area of shaded region"=1386+18`
`∴ "Area of shaded region"=1404`
Therefore, area of the shaded region is `1404 cm^2`
APPEARS IN
संबंधित प्रश्न
The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
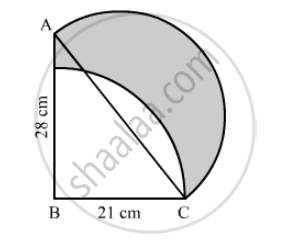
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
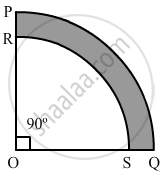
In the given figure, PQRS represents a flower bed. If OP = 21 m and OR = 14 m, find the area of the flower bed.
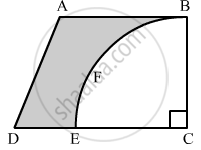
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
The area of a circle is 1386 sq.cm; find its circumference.
How much distance, in metres, a wheel of 25 cm radius will cover if it rotates 350 times?
