Advertisements
Advertisements
प्रश्न
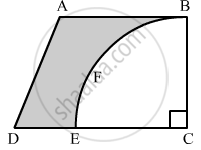
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
उत्तर
Since, BFEC is a quarter of a circle.
Hence, BC = EC = 3.5 cm
Now, DC = DE + EC = 2 + 3.5 = 5.5 cm
Area of shaded region = Area of the trapezium ABCD − Area of the quadrant BFEC
`= 1/2xx("AB" + "DC")xx"BC" - 1/4xxpi("EC")^2`
`=1/2xx(3.5+3.5)xx3.5-1/4xx22/7xx(3.5)^2`
= 6.125 cm2\
Hence, the area of the shaded region is 6.125 cm2 .
APPEARS IN
संबंधित प्रश्न
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the length of the arc. (Use π = `22/7`)
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
If the perimeter of a semi-circular protractor is 36 cm, then its diameter is
If the area of a sector of a circle is `5/18` of the area of the circle, then the sector angle is equal to
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

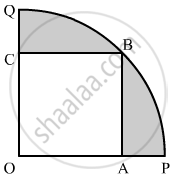
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
The area of a circle is 1386 sq.cm; find its circumference.
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
