Advertisements
Advertisements
प्रश्न
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
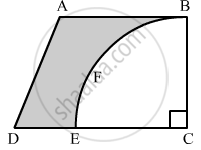
उत्तर
Since, BFEC is a quarter of a circle.
Hence, BC = EC = 3.5 cm
Now, DC = DE + EC = 2 + 3.5 = 5.5 cm
Area of shaded region = Area of the trapezium ABCD − Area of the quadrant BFEC
`= 1/2xx("AB" + "DC")xx"BC" - 1/4xxpi("EC")^2`
`=1/2xx(3.5+3.5)xx3.5-1/4xx22/7xx(3.5)^2`
= 6.125 cm2\
Hence, the area of the shaded region is 6.125 cm2 .
APPEARS IN
संबंधित प्रश्न
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
The area of a parallelogram is `392m^2` . If its altitude is twice the corresponding base, determined the base and the altitude.
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
From a thin metallic piece, in the shape of a trapezium ABCD, in which AB || CD and ∠BCD = 90°, a quarter circle BEFC is removed (in the following figure). Given AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining piece of the metal sheet.
If the radius of a circle is diminished by 10%, then its area is diminished by
The radii of two circles are 8 cm and 6 cm. Find the radius of the circle having area equal to the sum of the areas of the two circles.
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
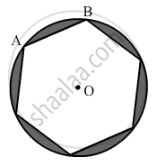
A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm, then find the total area of the design.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
How much distance, in metres, a wheel of 25 cm radius will cover if it rotates 350 times?
