Advertisements
Advertisements
Question
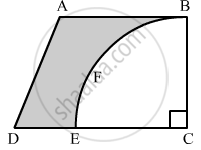
From a thin metallic piece in the shape of a trapezium ABCD in which AB || CD and ∠BCD = 90°, a quarter circle BFEC is removed. Given, AB = BC = 3.5 cm and DE = 2 cm, calculate the area of remaining (shaded) part of metal sheet.
Solution
Since, BFEC is a quarter of a circle.
Hence, BC = EC = 3.5 cm
Now, DC = DE + EC = 2 + 3.5 = 5.5 cm
Area of shaded region = Area of the trapezium ABCD − Area of the quadrant BFEC
`= 1/2xx("AB" + "DC")xx"BC" - 1/4xxpi("EC")^2`
`=1/2xx(3.5+3.5)xx3.5-1/4xx22/7xx(3.5)^2`
= 6.125 cm2\
Hence, the area of the shaded region is 6.125 cm2 .
APPEARS IN
RELATED QUESTIONS
From a circular piece of cardboard of radius 3 cm two sectors of 900 have been cutoff . Find the perimeter of the remaining portion nearest hundredth centimeters ( `"Take" pi = 22/ 7`).
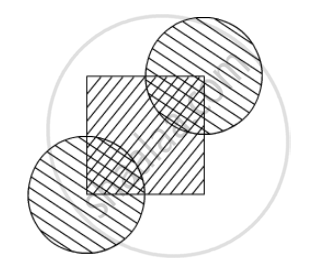
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
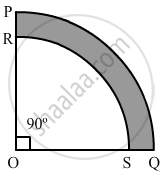
In the given figure, PQRS represents a flower bed. If OP = 21 m and OR = 14 m, find the area of the flower bed.
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
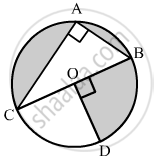
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of shaded region.
The area of a sector of a circle with radius r, making an angle of x° at the centre is
The given figures show a rectangle ABCD inscribed in a circle as shown alongside.
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.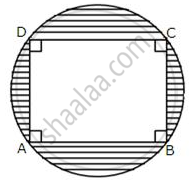
Area of the circle obtained in 196 m2 is ______.
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
