Advertisements
Advertisements
प्रश्न
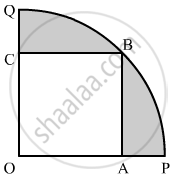
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
उत्तर
Construction: Join OB
In right triangle AOB
OB2 = OA2 + AB2
= 202 + 202
= 400 + 400
= 800
∴OB2 = 800
Area of the shaded region = Area of quadarant OPBQ - Area of square OABC
`=1/4pi("OB")^2 - ("OA")^2`
`=1/4xx3.14xx800-400`
= 628 - 400
= 228 cm2
Hence, the area of the shaded region is 228 cm2.
APPEARS IN
संबंधित प्रश्न
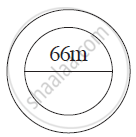
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (π = 3.14)
The base of an isosceles triangle measures 80 cm and its area is 2 `360 . cm^2` Find the perimeter of the triangle.
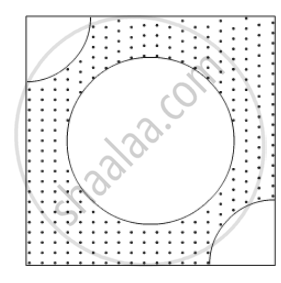
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
The diameter of a coin is 1 cm (in the following figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).
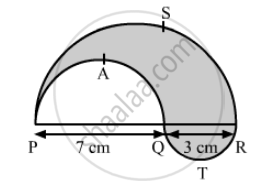
In the the following figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.
If the radius of a circle is diminished by 10%, then its area is diminished by
The area of the largest triangle that can be inscribed in a semi-circle of radius r is
The area of a circular path of uniform width h surrounding a circular region of radius r is
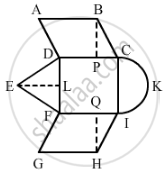
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centers is 10 cm. Find the radii of the two circles.
