Advertisements
Advertisements
Question
In the following figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and Δ CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
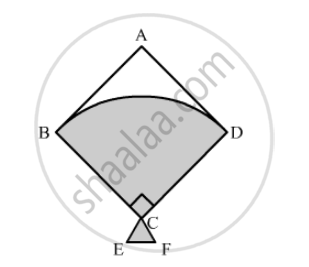
Solution
We will find the area of the shaded region as shown below,
Area of the shaded region = area of quadrant + area of isosceles triangle ……..(1)
`∴" Area of shaded region"=90/360xxpixx42^2+1/2xx6xx6`
`∴" Area of shaded region"=1/4xxpixx42^2+1/2xx36`
Substituting `pi=22/7` we get,
`∴ "Area of shaded region"=1/4xx22/7xx42^2+1/2xx36`
`∴ "Area of shaded region"=1/2xx11xx6xx42+18`
`∴ "Area of shaded region"=11xx3xx42+18`
`∴ "Area of shaded region"=1386+18`
`∴ "Area of shaded region"=1404`
Therefore, area of the shaded region is `1404 cm^2`
APPEARS IN
RELATED QUESTIONS
A 36-m-long, 15-m-borad verandah is to be paved with stones, each measuring 6dm by 5 dm. How many stones will be required?
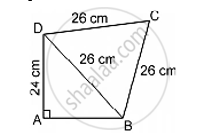
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

The perimeter of a certain sector of a circle of radius 6.5 cm in 31 cm. Find the area of the sector.
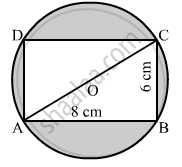
Find the area of the shaded region in the given figure, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle.
The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm2, find the area of the smaller circle.
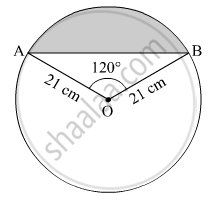
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.


