Advertisements
Advertisements
Question
A 36-m-long, 15-m-borad verandah is to be paved with stones, each measuring 6dm by 5 dm. How many stones will be required?
Solution
`Area of the verandah = "Length xx Breadth" = 36 xx15 = 540 m^2` Length of the stone = 6 dm = 0. 6 m
Breadth of the stone = 5 dm = 0.5 m
Area of one stone= `0.6xx0.5=0.3m^2`
=`540/0.3`
= `1800`
Thus, 1800 stones will be required to pave the verandah.
APPEARS IN
RELATED QUESTIONS
The length of a rectangular park is twice its breadth and its perimeter is 840 m. Find the area of the park.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
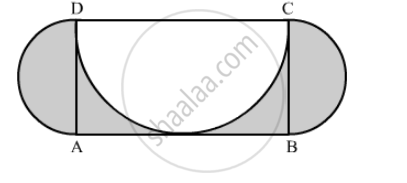
In the following figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi-circles are drawn as shown in the figure. Find the area of the shaded region.
Write the formula for the area of a sector of angle \[\theta\] (in degrees) of a circle of radius r.
In the following figure, the area of the segment PAQ is

The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
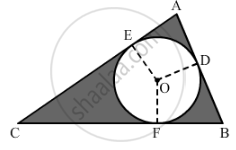
In the given figure, ∆ABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incircle of ∆ABC.
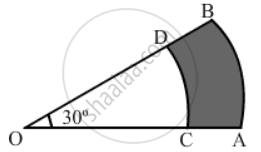
In the given figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
The following figure shows a square cardboard ABCD of side 28 cm. Four identical circles of the largest possible sizes are cut from this card as shown below.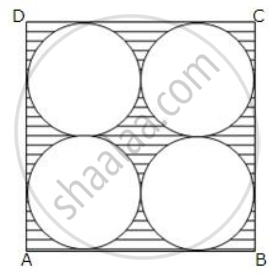
Find the area of the remaining card-board.
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
