Advertisements
Advertisements
प्रश्न
A 36-m-long, 15-m-borad verandah is to be paved with stones, each measuring 6dm by 5 dm. How many stones will be required?
उत्तर
`Area of the verandah = "Length xx Breadth" = 36 xx15 = 540 m^2` Length of the stone = 6 dm = 0. 6 m
Breadth of the stone = 5 dm = 0.5 m
Area of one stone= `0.6xx0.5=0.3m^2`
=`540/0.3`
= `1800`
Thus, 1800 stones will be required to pave the verandah.
APPEARS IN
संबंधित प्रश्न
Find the area and perimeter of an isosceles right angled triangle, each of whose equal sides measure 10cm.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
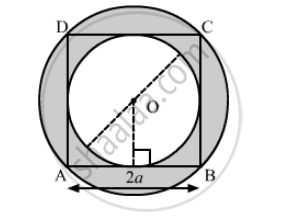
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
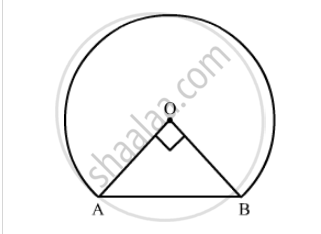
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
The area of a circle whose area and circumference are numerically equal, is
If diameter of a circle is increased by 40%, then its area increase by
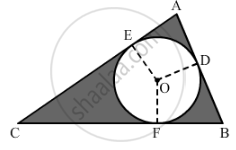
In the given figure, ∆ABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incircle of ∆ABC.
Is the area of the circle inscribed in a square of side a cm, πa2 cm2? Give reasons for your answer.
