Advertisements
Advertisements
प्रश्न
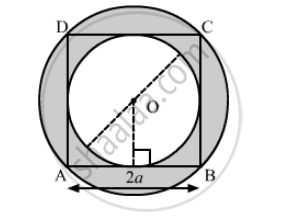
In the following figure, ABCD is a square of side 2a, Find the ratio between
(i) the circumferences
(ii) the areas of the in circle and the circum-circle of the square.
उत्तर
We have a square ABCD having`AB=2c`. From the given diagram we can observe that,
Radius of incircle `(r_1)=a`
Radius of circumcircle `(r_2)=sqrt2a`
(i) We have to find the ratio of the circumferences of the two circles. So the required ratio is,
=` "Perimeter of inner circle "/"Perimeter of circumcircle" `
`=(2pi(a))/(2 pi(sqrt2a))`
`= 1/sqrt2`
(ii) We have to find the ratio of the areas of the two circles. So the required ratio is,
`= "Area of inner circle"/"Area of circumcircle"`
`= (pi(a)^2)/(pi(sqrt2a)^2)`
`=1/2`
APPEARS IN
संबंधित प्रश्न
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
A footpath of uniform width runs all around the inside of a rectangular field 54m long and 35 m wide. If the area of the path is `420m^2` , find the width of the path.
From a circular piece of cardboard of radius 3 cm two sectors of 900 have been cutoff . Find the perimeter of the remaining portion nearest hundredth centimeters ( `"Take" pi = 22/ 7`).
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
The area of a circle whose area and circumference are numerically equal, is
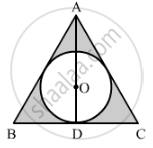
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use `sqrt(3)= 1.73, pi = 3.14]`
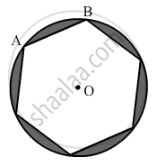
A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm, then find the total area of the design.
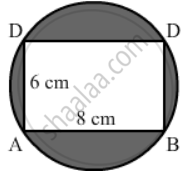
In the given figure, ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm. If π = 3.14, then the area of the shaded region is:
A 7m wide road surrounds a circular garden whose area is 5544m2. Find the area of the road and the cost of tarring it at the rate of Rs.150 per m2.
Find the area of the biggest circle that can be cut from a rectangular piece 44cm by 28cm. also, find the area of the paper left after cutting out the circle.
