Advertisements
Advertisements
प्रश्न
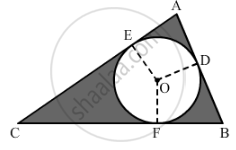
In the given figure, ∆ABC is right-angled at A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and O is the centre of the incircle of ∆ABC.
उत्तर
Using Pythagoras' theorem for triangle ABC, we have:
CA2 + AB2 = BC2
CA` = sqrt("BC"^2 - "AB"^2)`
`=sqrt(100-36)`
`=sqrt(64)`
= 8 cm
Now, we must find the radius of the incircle. Draw OE, OD and OF perpendicular to AC, AB and BC, respectively.
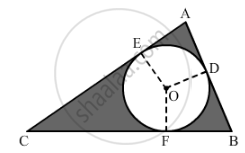
Consider quadrilateral AEOD.
Here,
EO = OD(Both are radii.)
Because the circle is an incircle, AE and AD are tangents to the circle.
∠AEO = ∠ADO = 90°
Also,
∠A = 90°
Therefore, AEOD is a square.
Thus, we can say that AE = EO = OD = AD = r.
CE = CF = 8 - r
BF = BD = 6 - r
CF + BF = 10
⇒ (8 - r)+(6-r) = 10
⇒ 14 - 2r = 10
⇒ r = 2 cm
Area of the shaded part = Area of the triangle-- Area of the circle
`= {1/2xx6xx8} - {pixx2xx2}`
= 24 - 12.56
= 11.44 cm2
APPEARS IN
संबंधित प्रश्न
A carpet is laid on floor of a room 8 m by 5 m. There is border of constant width all around the carpet. If the area of the border is `12m^2` find its width.
Find the area of the following figure, in square cm, correct to one place of decimal. (Take π = 22/7).
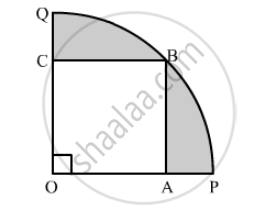
In the following figure a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
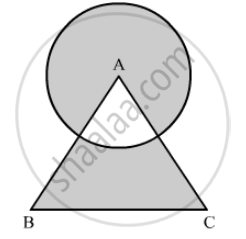
In the following figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
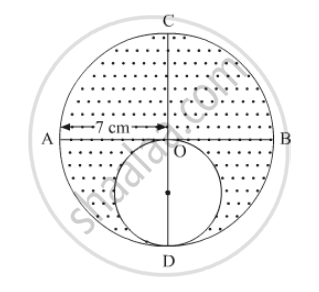
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
The hour hand of a clock is 6 cm long. The area swept by it between 11.20 am and 11.55 am is
A square is inscribed in a circle of radius 7 cm. Find the area of the square.
Two circles touch each other externally. The sum of their areas is 58πcm2 and the distance between their centres us 10cm. Find the radii of the two circles.
