Advertisements
Advertisements
प्रश्न
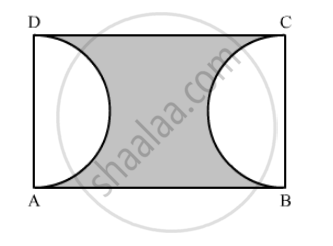
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
उत्तर
We know that we can cut two circular pieces of equal radii and maximum area from the rectangular cardboard whose diameter is equal to the width of the rectangular cardboard.
∴ Radii of two circuar pieces = Half of the width of the rectangular cardboard = 3.5 cm
Now,
Area of remaining cardboard = Area of rectangular cardboard − 2 ⨯ Area of circular piece having radius 3.5 cm
\[= 14 \times 7 - 2\left( \frac{22}{7} \times 3 . 5 \times 3 . 5 \right)\]
\[ = 98 - 77\]
\[ = 21 {cm}^2\]
Hence, the area of the remaining cardboard is 21 cm2
APPEARS IN
संबंधित प्रश्न
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9 cm, CD = 12 cm, ∠ACB=90° and AC = 15 cm.

In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
If AB is a chord of length \[5\sqrt{3}\] cm of a circle with centre O and radius 5 cm, then area of sector OAB is
The hour hand of a clock is 6 cm long. The area swept by it between 11.20 am and 11.55 am is
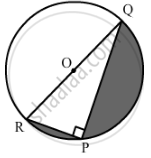
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
In the given figure, an equilateral triangle has been inscribed in a circle of radius 4 cm. Find the area of the shaded region.

A square is inscribed in a circle of radius 7 cm. Find the area of the square.
If the radius of a circle is doubled, its area becomes ____________.
