Advertisements
Advertisements
प्रश्न
In the given figure, an equilateral triangle has been inscribed in a circle of radius 4 cm. Find the area of the shaded region.

उत्तर
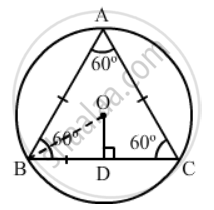
Draw
OD ⊥ BC
.
Because ΔABC is equilateral, ∠A = ∠B = ∠C = 60° .
Thus, we have:
∠OBD = 30°
`⇒ "OD"/"OB" = sin 30°`
`=> "OD"/"OB" = 1/2`
`=>"OB" = (1/2)`
`=> "OD" = (1/2xx4)"cm" [therefore "OB" = "radius"]`
⇒ OD =2 cm
⇒ BD2 = (OB2 - OD2) [By Pythagoras 'Therom']
⇒ BD2 = (42 - 22) cm2
⇒ BD2 = (16 - 4) cm2
⇒ BD2 = 12 cm2
`⇒ "BD" = 2sqrt(3)`
Also
BC = 2 × BD
`=>(2xx2sqrt(3))`
`=4sqrt(3)`
∴ Area of the shaded region = (Area of the circle) - (Area of Δ)
`=|(3.14xx4xx4)-(sqrt(3)/4xx4sqrt(3)xx4sqrt(3))|"cm"^2`
`= |50.24 - (12xx1.73)| "cm"^2`
= (50.24 - 20.76) cm2
= 29.48 cm2
APPEARS IN
संबंधित प्रश्न
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
A 80 m by 64 m rectangular lawn has two roads, each 5 m wide, running through its middle, one parallel to its length and the other parallel to its breadth. Find the cost of gravelling the reads at ₹` 40 per m^2`
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. `[\text{Use}pi=22/7]`
An archery target has three regions formed by three concentric circles as shown in figure. If the diameters of the concentric circles are in the ratios 1 : 2 : 3, then find the ratio of the areas of three regions.
A chord of a circle of radius 20 cm sub tends an angle of 900 at the centre . Find the area of the corresponding major segment of the circle
( Use \[\pi = 3 . 14\])
The hour hand of a clock is 6 cm long. The area swept by it between 11.20 am and 11.55 am is
A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of the pendulum.
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
Find the area of the dining table whose diameter is 105 cm
