Advertisements
Advertisements
प्रश्न
In the given figure, an equilateral triangle has been inscribed in a circle of radius 4 cm. Find the area of the shaded region.

उत्तर
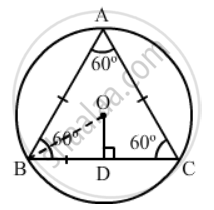
Draw
OD ⊥ BC
.
Because ΔABC is equilateral, ∠A = ∠B = ∠C = 60° .
Thus, we have:
∠OBD = 30°
`⇒ "OD"/"OB" = sin 30°`
`=> "OD"/"OB" = 1/2`
`=>"OB" = (1/2)`
`=> "OD" = (1/2xx4)"cm" [therefore "OB" = "radius"]`
⇒ OD =2 cm
⇒ BD2 = (OB2 - OD2) [By Pythagoras 'Therom']
⇒ BD2 = (42 - 22) cm2
⇒ BD2 = (16 - 4) cm2
⇒ BD2 = 12 cm2
`⇒ "BD" = 2sqrt(3)`
Also
BC = 2 × BD
`=>(2xx2sqrt(3))`
`=4sqrt(3)`
∴ Area of the shaded region = (Area of the circle) - (Area of Δ)
`=|(3.14xx4xx4)-(sqrt(3)/4xx4sqrt(3)xx4sqrt(3))|"cm"^2`
`= |50.24 - (12xx1.73)| "cm"^2`
= (50.24 - 20.76) cm2
= 29.48 cm2
APPEARS IN
संबंधित प्रश्न
The dimensions of a room are 14 m x 10 m x 6.5 m There are two doors and 4 windows in the room. Each door measures 2.5 m x 1.2 m and each window measures 1.5 m x 1 m. Find the cost of painting the four walls of the room at ₹ `35perm^2` .
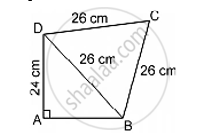
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
From a circular piece of cardboard of radius 3 cm two sectors of 900 have been cutoff . Find the perimeter of the remaining portion nearest hundredth centimeters ( `"Take" pi = 22/ 7`).
What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
What is the length (in terms of π) of the arc that subtends an angle of 36° at the centre of a circle of radius 5 cm?
In the following figure, If ABC is an equilateral triangle, then shaded area is equal to
From a rectangular sheet of paper ABCD with AB = 40 cm and AD = 28 cm, a semicircular portion with BC as diameter is cut off. Find the area of the remaining paper.
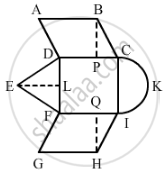
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
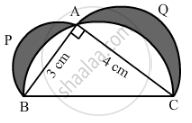
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
The length of the minute hand of a clock is 21 cm. The area swept by the minute hand in 10 minutes is
