Advertisements
Advertisements
प्रश्न
The minute hand of a clock is 12 cm long. Find the area of the face of the clock described by the minute hand in 35 minutes.
उत्तर
Angle described by the minute hand in 60 minutes
= 360°
Angle described by the minute hand in 35 minutes `= (360/60xx35)°`
= 210°
Now,
r = 12 cm and θ = 210°
∴ Required area described by the minute hand in 35 minutes = Area of the sector where
r = 12 cm and θ = 210°
`=(pi"r"^2theta)/360`
`=(22/7xx12xx12xx210/360) "cm"^2`
= 264 cm2
APPEARS IN
संबंधित प्रश्न
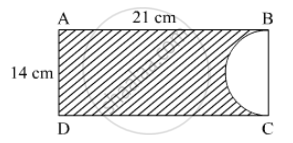
In the given figure, ABCD is rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the following figure). Find the area of the remaining sheet. (Take `pi = 22/7`)

Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is `pih(2r+h)`
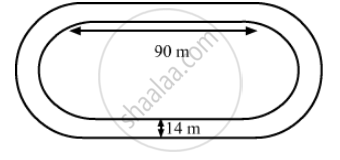
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
If the area of a square is same as the area of a circle, then the ratio of their perimeters, in terms of π, is
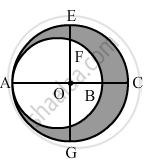
In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10, find the area of the shaded region.
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
A chord of a circle of radius 14 cm a makes a right angle at the centre. Find the area of the sector.
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is ______.
