Advertisements
Advertisements
प्रश्न
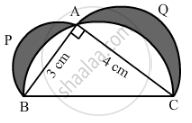
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
उत्तर
In triangle ΔABC, we have:
`BC = sqrt("AB"^2 + "AC"^2)`
`=sqrt(9+16)`
`=sqrt(25)`
= 5 cm
Ar(shaded part) = Ar(ΔABC) + Ar(semicircle APB) + Ar(semicircle AQC) - Ar(semicircle BAC)
`= (1/2xx3xx4)+(1/2pixx1.5xx1.5)+(1/2pixx2xx2)-(1/2pixx2.5xx2.5)`
`= {6 + 1/2pi(4+9/4-25/4)}`
= 6 + 0
= 6 cm2
APPEARS IN
संबंधित प्रश्न
A road which is 7 m wide surrounds a circular park whose circumference is 352 m . Find the area of the road .
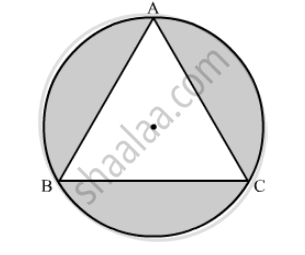
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
A wire can be bent in the form of a circle of radius 56 cm. If it is bent in the form fo a square, then its area will be
If the area of a circle is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm, then diameter of the large circle (in cm) is
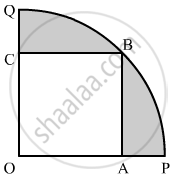
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
A racetrack is in the form of a ring whose inner circumference is 352 m and outer circumference is 396 m. Find the width and the area of the track.
The radii of two circles are in the ratio 3: 8. If the difference between their areas is 2695π cm2, find the area of the smaller circle.
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
