Advertisements
Advertisements
प्रश्न
A pendulum swings through an angle of 30° and describes an arc 8.8 cm in length. Find the length of the pendulum.
उत्तर
Given:
Length of the arc = 8.8 cm
And,
θ = 30°
Now,
Length of the arc` = (2pi"r"theta)/360`
`=> 8.8 =(2xx22/7xx"r"xx360)/(360)`
`=>"r" = (8.8xx360xx7)/(44xx30)`
∴ r = 16.8 cm
Length of the pendulum = 16.8 cm
APPEARS IN
संबंधित प्रश्न
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
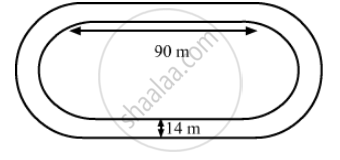
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
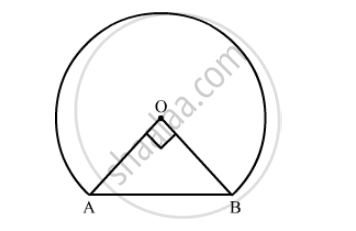
In the following figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
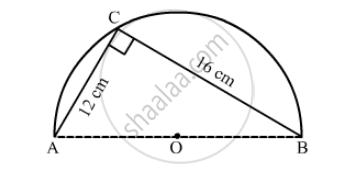
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the area of the cross-section.
If AB is a chord of length \[5\sqrt{3}\] cm of a circle with centre O and radius 5 cm, then area of sector OAB is
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
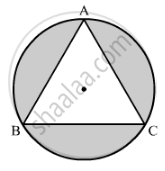
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
A sprinkler placed at the centre of a flower garden sprays water covering a circular area. If the area watered is 1386 cm2, find its radius and diameter
The radii of the two circles are 4 cm and 3 cm respectively. The diameter of the circle having an area equal to the sum of the areas of the two circles (in cm) is ____________.
