Advertisements
Advertisements
प्रश्न
The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
उत्तर
Cost of fencing the lawn Rs` 28000`
Let lbe the length of each side of the lawn. Then, the perimeter is 4. l We know
`"Cost"= "Rate"xx "Perimeter"`
⇒`28000=14 xx41`
⇒` 28000=56l`
Or,` l=28000/56=500m`
Area of the square lawn=`500xx500=250000 m^2`
Cost of moving `100 m^2` of the lawn= `Rs 54`
Cost of moving `1m^2` of the lawn=Rs `54/100`
∴ Cost of moving `250000 m^2` of the lawn =` (250000xx54)/100`= `Rs 135000`
APPEARS IN
संबंधित प्रश्न
A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.

ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
If the perimeter of a semi-circular protractor is 36 cm, then its diameter is
In the following figure, the area of the segment PAQ is

If π is taken as `22/7` the distance (in metres) covered by a wheel of diameter 35 cm, in one revolution, is
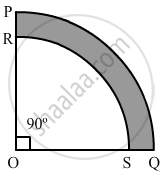
In the given figure, PQRS represents a flower bed. If OP = 21 m and OR = 14 m, find the area of the flower bed.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor segments (given, π = 3.14) is
The area of the circle is 154 cm2. The radius of the circle is ______.
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
