Advertisements
Advertisements
प्रश्न
The diameters of three wheels are in the ratio 2 : 4 : 8. If the sum of the circumferences of these circles be 132 cm, find the difference between the areas of the largest and the smallest of these wheels.
उत्तर
Let the diameters of three wheel be
d1 = 2x ⇒ r1 = x
d2 = 4x ⇒ r2 = 2x
d3 = 8x ⇒ r3 = 4x
Now,
2πr1 + 2πr2 + 2πr3 = 132
⇒ 2π(r1 + r2 + r3) = 132
⇒ x + 2x + 4x = `66 xx (7)/(22)`
⇒ 7x = 21
⇒ x = 3cm
∴ DIfference between the areas of the largest and the smallest wheels
= πr32 - πr12
= π(4 x 3)2 - π(3)2
= 144π - 9π
= 135π
= `135 xx (22)/(7)`
= 424.29cm2.
APPEARS IN
संबंधित प्रश्न
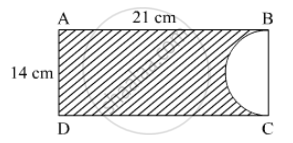
In the given figure, ABCD is rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
One side of a rectangle is 12 cm long and its diagonal measure 37 cm. Find the other side and the area of the rectangle.
The area of rectangle is `192cm^2` and its perimeter is 56 cm. Find the dimensions of the rectangle.
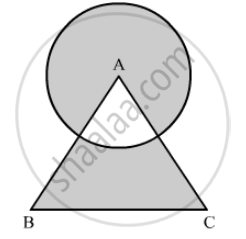
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

If the circumference of a circle increases from 4π to 8π, then its area is
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
A square is inscribed in a circle of radius 7 cm. Find the area of the square.
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
Area of the circle obtained in 196 m2 is ______.
