Advertisements
Advertisements
प्रश्न
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
उत्तर
In a circle
Circumference = Sum of circumferences of two circle of radii 15 cm and 13 cm
Now circumference of first smaller circle = 2πr
= `2 xx 22/7 xx 15 = 660/7` cm
Circumference of the second smaller circle
= `2 xx 22/7 xx 13 = 572/7` cm
∴ Circumference of the bigger circle
= `660/7 + 572/7 = 1232/7` cm
Let R be its radius, then
`2pi"R" = 1232/7 ⇒ (2 xx 22)/7 "R" = 1232/7`
⇒ R = `1232/7 xx 7/44 = 28` cm
∴ Area of the circle = `pi"R"^2`
= `22/7 xx 28 xx 28 "cm"^2 = 2464` cm2
APPEARS IN
संबंधित प्रश्न
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
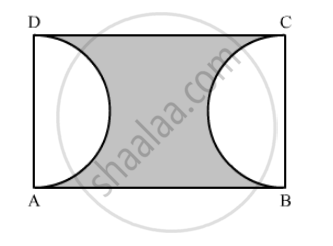
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the area of the shaded region.
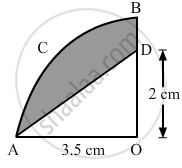
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
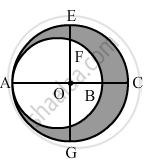
In the given figure, O is the centre of the bigger circle, and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10, find the area of the shaded region.
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
Find the area of a circle of radius 30 cm (use π = 3.14).
Is the area of the circle inscribed in a square of side a cm, πa2 cm2? Give reasons for your answer.
