Advertisements
Advertisements
प्रश्न
In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm, ∠AED = 90° and DE = 42 cm. A semicircle is drawn, taking BC as diameter. Find the area of the shaded region.
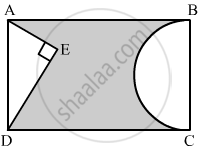
उत्तर
We know that the opposite sides of a rectangle are equal
AD = BC = 70 cm
In right triangle AED
AE2 = AD2 − DE2
= (70)2 − (42)2
= 4900 − 1764
= 3136
∴ AE2 = 3136
⇒ AE = 56
= Area of the shaded region = Area of rectangle − (Area of triangle AED + Area of semicircle)
`= "AB"xx"BC"-[1/2xx"AE"xx"DE" + 1/2pi("BC"/2)^2]`
`= 80xx70-[1/2xx56xx42+1/2xx22/7(70/2)^2]`
= 5600 - 3101
= 2499 cm2
Hence, the area of shaded region is 2499 cm2
APPEARS IN
संबंधित प्रश्न
A path of width 3.5 m runs around a semi-circular grassy plot whose perimeter is 72 m . Find the area of the path .
`("Use" pi= 22/7) `
Find the ratio of the area of the circle circumscribing a square to the area of the circle inscribed in the square .
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
The area of a circle whose area and circumference are numerically equal, is
A rope by which a cow is tethered is increased from 16 m to 23 m. How much additional ground does it have now graze?
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
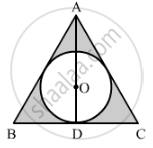
In the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use `sqrt(3)= 1.73, pi = 3.14]`
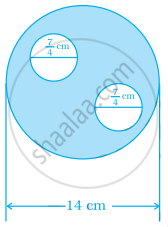
Find the area of the shaded region:
A table cover of dimensions 3 m 25 cm × 2 m 30 cm is spread on a table. If 30 cm of the table cover is hanging all around the table, find the area of the table cover which is hanging outside the top of the table. Also find the cost of polishing the table top at ₹ 16 per square metre.
