Advertisements
Advertisements
प्रश्न
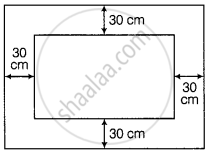
A table cover of dimensions 3 m 25 cm × 2 m 30 cm is spread on a table. If 30 cm of the table cover is hanging all around the table, find the area of the table cover which is hanging outside the top of the table. Also find the cost of polishing the table top at ₹ 16 per square metre.
उत्तर
To find the cost of polishing the table top, we have to find its area for which we require its length and breadth.
Given, length of cover = 3 m 25 cm = 3.25 m and breadth of cover = 2 m 30 cm = 2.30 m
∴ Area of the table cover = 3.25 × 2.30 = 7.475 m2
Since, 30 cm width of cloth is outside the table an each side.
∴ Length of the table = 3.25 – 2 × 0.30 = 2.65 m ......`[∵ 1 cm = 1/100 m]`
and breadth of the table = 2.30 – 2 × 0.30 = 1.70 m
∴ Area of the top of the table = (2.65 × 1.70) m2
= 4.505 m2
Avea of the hanging table cover = Area of table cover – Area of the top of the table
= (7.475 – 4.505) m2
= 2.97 m2
It is given that, the cost of polishing the table top is at the rate of ₹ 16 per square metre
Therefore, cost of polishing the top = Area × Rate per square metre
= 4.505 × 16
= ₹ 7.208
APPEARS IN
संबंधित प्रश्न
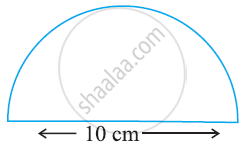
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
A room 4.9 m long and 3.5 m board is covered with carpet, leaving an uncovered margin of 25 cm all around the room. If the breadth of the carpet is 80 cm, find its cost at ₹ 80 per metre.
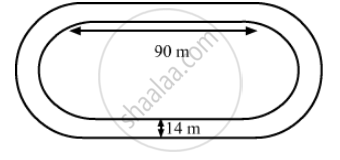
The inside perimeter of a running track (shown in the following figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide. find the area of the track. Also find the length of the outer running track.
ABCDEF is a regular hexagon with centre O (in the following figure). If the area of triangle OAB is 9 cm2, find the area of : (i) the hexagon and (ii) the circle in which the haxagon is incribed.
What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
The minute hand of a clock is 15 cm long. Calculate the area swept by it in 20 minutes.
In the given figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region. [Use π= 3.14]

The area of a circle is 98.56 cm2. Find its circumference.
A chord of a circle of radius 14 cm a makes a right angle at the centre. Find the area of the sector.
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
