Advertisements
Advertisements
Question
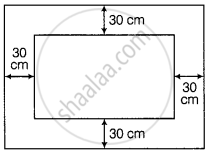
A table cover of dimensions 3 m 25 cm × 2 m 30 cm is spread on a table. If 30 cm of the table cover is hanging all around the table, find the area of the table cover which is hanging outside the top of the table. Also find the cost of polishing the table top at ₹ 16 per square metre.
Advertisements
Solution
To find the cost of polishing the table top, we have to find its area for which we require its length and breadth.
Given, length of cover = 3 m 25 cm = 3.25 m and breadth of cover = 2 m 30 cm = 2.30 m
∴ Area of the table cover = 3.25 × 2.30 = 7.475 m2
Since, 30 cm width of cloth is outside the table an each side.
∴ Length of the table = 3.25 – 2 × 0.30 = 2.65 m ...`[∵ 1 cm = 1/100 m]`
And breadth of the table = 2.30 – 2 × 0.30 = 1.70 m
∴ Area of the top of the table = (2.65 × 1.70) m2
= 4.505 m2
Area of the hanging table cover = Area of table cover – Area of the top of the table
= (7.475 – 4.505) m2
= 2.97 m2
It is given that, the cost of polishing the table top is at the rate of ₹ 16 per square metre.
Therefore, cost of polishing the top = Area × Rate per square metre
= 4.505 × 16
= ₹ 7.208
APPEARS IN
RELATED QUESTIONS
The area of a rectangular plot is ` 462m^2` and is length is 28 m. Find its perimeter.
Find the area of the following figure, in square cm, correct to one place of decimal. (Take π = 22/7).
A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (the following figure). Find the radius of the inscribed circle and the area of the shaded part.
A child makes a poster on a chart paper drawing a square ABCD of side 14 cm. She draws four circles with centre A, B, C and D in which she suggests different ways to save energy. The circles are drawn in such a way that each circle touches externally two of the three remaining circles (in the following figure). In the shaded region she write a message 'Save Energy'. Find the perimeter and area of the shaded region.
(Use π = 22/7)
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to the sum of the areas of the two given circles.
The minute hand of a clock is 8 cm long. Find the area swept by the minute hand between 8.30 a.m. and 9.05 a.m.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
What is the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40cm and 9cm?
