Advertisements
Advertisements
प्रश्न
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
उत्तर
If a square is inscribed in a circle, then the diagonals of the square are diameters of the circle.
Let the diagonal of the square be d cm.
Thus, we have:
Radius , `"r" = "d"/2 "cm"`
Area of the circle = πr2
`= pi"d"^2/4 "cm"^2`
We know ;
`"d"= sqrt(2)xx"Side" `
`=> "Side" = ("d"/sqrt(2)) "cm"`
Area of the the circle = πr2
`=pi"d"^2/4 "cm"^2`
We know ;
`d = sqrt(2)xx"side"`
`⇒ "Side" = "d"/sqrt(2) "cm"`
Area of the square`=("Side")^2`
`=("d"/sqrt(2))^2`
`= "d"^2/2 "cm"^2`
Ratio of the area of the circle to that of the square:
`= (pi"d"^2/4)/("d"^2/2)`
`= pi/2 `
Thus, the ratio of the area of the circle to that of the square is π : 2
APPEARS IN
संबंधित प्रश्न
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

What is the area of a sector of a circle of radius 5 cm formed by an arc of length 3.5 cm?
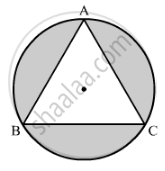
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3)" cm"^2`. If the same wire is bent into the form of a circle, what will be the area of the circle?
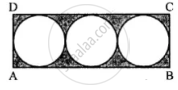
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
The sum of the radii of two circles is 10.5 cm and the difference of their circumferences is 13.2 cm. Find the radii of the two circles.
If the perimeter of a semicircular protractor is 72 cm where `pi = 22/7`, then the diameter of protractor is ____________.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
