Advertisements
Advertisements
प्रश्न
In the following figure, a rectangle ABCD enclosed three circles. If BC = 14 cm, find the area of the shaded portion (Take π = 22/7)
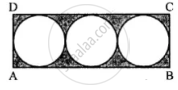
उत्तर
To calculate the area of the shaded portion, we need to subtract the total area of the three circles from the area of the rectangle.
- Length of BC (Rectangle's width): 14 cm
- The three circles are identical, and their diameters fit perfectly along the length of the rectangle (AD).
Thus: Diameter of each circle = `("Length of AD (Rectangle)")/("Number of circles")"`
`= 14/3 = 14/3 cm`
Radius of each circle = `"Diameter"/2 = 14/6 = 7/3 cm`
Step 1: Area of the rectangle
Area of Rectangle = Length × Width = AD × BC.
AD = 14 cm, BC = 14 cm.
Area of Rectangle = 14 × 14 = 96 cm2
Step 2: Total area of the three circles
Area of one circle = πr2.
`r = 7/3 cm, pi=22/7`
Area of one circle `= 22/7xx(7/3)^2=22/7xx49/9=1078/63 cm^2`
Total Area of Circles `= 3xx1078/63 = 3234/63 = 51.33 cm^2`
Step 3: Area of the shaded portion
Shaded Area = Area of Rectangle − Total Area of Circles.
Shaded Area = 196 − 51.33 = 144.67 cm2.
The area of the shaded portion is approximately: 144.67 cm2
APPEARS IN
संबंधित प्रश्न
A rectangular plot measure 125 m by 78 m. It has gravel path 3 m wide all around on the outside. Find the area of the path and the cost of gravelling it at` ₹ 75 per m^2`
The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
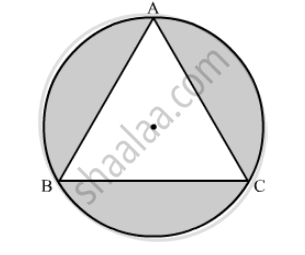
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
If the circumference of two circles are in the ratio 2 : 3, what is the ratio of their areas?
The area of a sector whose perimeter is four times its radius r units, is
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
A circular disc of radius 6 cm is divided into three sectors with central angles 90°,120° and 150°. What part of the whole circle is the sector with central angle 150°? Also, calculate the ratio of the areas of the three sectors.
If the radius of a circle is tripled, the area becomes ______.
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.


