Advertisements
Advertisements
प्रश्न
A rectangular plot measure 125 m by 78 m. It has gravel path 3 m wide all around on the outside. Find the area of the path and the cost of gravelling it at` ₹ 75 per m^2`
उत्तर
The plot with the gravel path is shown in the figure.
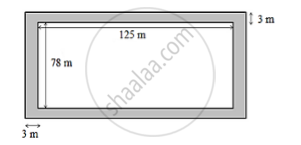
Area of the rectangular plot=`lxxb`
Area of the rectangular plot=`125xx78=9750m^2`
Length of the park including the path=`125+6=131m`
Breadth of the park including the path=`78+6=84`
Area of the plot including the path
=`131xx84`
=`11004m^2`
Area of the path=`11004-9750`
=`1254m^2`
Cost of gravelling `1m^2` of the path =Rs 75
Cost of gravelling`1254 m^2` of the path=`1254xx75`
=Rs `94050`
APPEARS IN
संबंधित प्रश्न
The cost of painting the four walls of a room 12 m long at `₹ 30 per m^2 is ₹ 7560 per m^2` and the cost of covering the floor with the mat at ₹` 25 per m^2 is ₹ 2700 `. find the dimensions of the room.
The area of a square filed is 8 hectares. How long would a man take to cross it diagonally by walking at the rate of 4 km per hour?
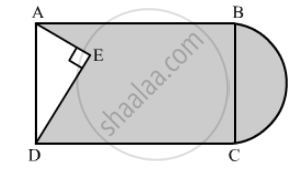
In the following figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π =]`22/7` [CBSE 2014]
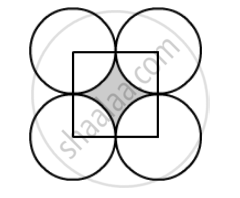
The diameter of a coin is 1 cm (in the following figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
If a wire is bent into the shape of a square, then the area of the square is 81 cm2. When wire is bent into a semi-circular shape, then the area of the semi-circle will be ______.
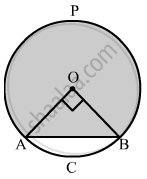
Find the area of the major segment APB of a circle of radius 35 cm and ∠AOB = 90°, as shown in the given figure.
A circle of the largest area is cut from a rectangular piece of cardboard with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
