Advertisements
Advertisements
प्रश्न
If a wire is bent into the shape of a square, then the area of the square is 81 cm2. When wire is bent into a semi-circular shape, then the area of the semi-circle will be ______.
विकल्प
22 cm2
44 cm2
77 cm2
154 cm2
उत्तर
If a wire is bent into the shape of a square, then the area of the square is 81 cm2. When wire is bent into a semi-circular shape, then the area of the semi-circle will be 77 cm2.
Explanation:
We have given that a wire is bent in the form of square of side a cm such that the area of the square is `81 cm^2`. If we bent the same wire in the form of a semicircle with radius r cm, the perimeter of the wire will not change.
∴ perimeter of the square = perimeter of semi circle
`4a=1/2 (2pir)+2r` ...(1)
We know that area of the square = 81 cm2
∴ a2 = 81
∴ a = 9
Now we will substitute the value of a in the equation (1),
`4xx9=1/2(2pi r)+2r`
`∴ 36=1/2(2pir)+2r`
`∴36=(pir)+2r`
`∴36=r(pi+2)`
Now we will substitute `pi=22/7`
`∴36=r(22/7+2)`
`∴36=r((22+14)/7)`
`∴36=r(36/7)`
Multiplying both sides of the equation by 7 we get, 36 × 7 = r × 36
Now we will divide both sides of the equation by 36 we get, r = 7
Therefore, radius of the semi circle is 7cm.
Now we will find the area of the semicircle.
Area of the semicircle = `1/2xxpir^2`
= `1/2xxpixx7^2`
= `1/2xx22/7xx7^2`
= 11 × 7
= 77
Therefore, the area of the semicircle is 77 cm2.
APPEARS IN
संबंधित प्रश्न
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed. (as shown in the following figure). Find the area of the remaining sheet. (Take `pi = 22/7`)

In the given figure, ΔABC is an equilateral triangle the length of whose side is equal to 10 cm, and ΔADC is right-angled at D and BD= 8cm. Find the area of the shaded region.

A footpath of uniform width runs all around the inside of a rectangular field 54m long and 35 m wide. If the area of the path is `420m^2` , find the width of the path.
The adjacent sides of a parallelogram are 32 cm and 24 cm. If the distance between the longer sides is 17.4 cm, find the distance between the shorter sides.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
The diameter of a coin is 1 cm (in the following figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).
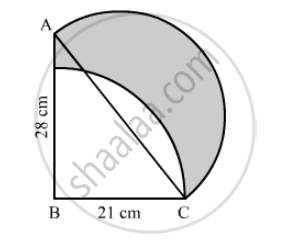
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
A chord of a circle of radius 14 cm a makes a right angle at the centre. Find the area of the sector.
In figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.
