Advertisements
Advertisements
प्रश्न
The adjacent sides of a parallelogram are 32 cm and 24 cm. If the distance between the longer sides is 17.4 cm, find the distance between the shorter sides.
उत्तर
Longer side = 32 cm
Shorter side = 24 cm
Let the distance between the shorter sides be x cm.
Area of a parallelogram = Longer side`xx`Distance between the longer sides = Shorter side`xx`Distance between the shorter sides
Or, `32xx17.4=24 xx x`
Or x= ` (32xx17.4)/24=23.2` cm
∴Distance between the shorter sides = `23.2 cm`
APPEARS IN
संबंधित प्रश्न
An arc subtends an angle of 90° at the centre of the circle of the radius 14 cm. Write the area of minor sector thus formed in terms of π.
The area of the largest triangle that can be inscribed in a semi-circle of radius r, is
In the following figure, the area of the shaded region is
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
ABCD is a field in the shape of a trapezium, AD || BC, ∠ABC = 90° and ∠ADC = 60°. Four sectors are formed with centres A, B, C and D, as shown in the figure. The radius of each sector is 14 m. Find the following:
- total area of the four sectors,
- area of the remaining portion, given that AD = 55 m, BC = 45 m and AB = 30 m.

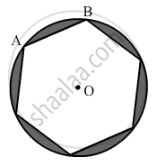
A round table cover has six equal designs as shown in the given figure. If the radius of the cover is 35 cm, then find the total area of the design.
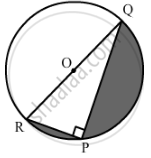
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
The ratio of the area of a circle to the area of its semicircle is
The area of the circle that can be inscribed in a square of side 6 cm is ______.
