Advertisements
Advertisements
प्रश्न
Find the perimeter and area of the shaded portion of the following diagram; give your answer correct to 3 significant figures. (Take π = 22/7).
उत्तर
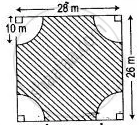
Area of rectangle = 28 m x 26 m = 728 m2
(i) Perimeter of the shaded position
= 2 x 28 + 2 x 26 - 4 x 20 + 2 x `22/7` x 10
= 56 + 52 - 80 + `440/7`
= 108 - 80 + 62.85
= 170.85 - 80
= 90.85 m.
(ii) Area of one corner (unshaded) = `1/4` π x (10)2
= `1/4` x (3.14)(100 m2)
= `314/4`
= 78.5 m2
∴ Area of 4 corners (unshaded) = 78.5 x 4 = 314 m2
∴ Area of the shaded portion = [728 - 314] m2 = 414 m2.
APPEARS IN
संबंधित प्रश्न
A hollow sphere of internal and external diameter 4cm and 8cm is melted into a cone of base diameter 8cm. Calculate height of cone?
A cylindrical tube of radius 12cm contains water to a depth of 20cm. A spherical ball is dropped into the tube and the level of the water is raised by 6.75cm.Find the radius of the ball .
A well with inner radius 4m is dug 14m deep earth taken out of it has been spread evenly all around a width of 3m it to form an embankment. Find the height of the embankment?
A petrol tank is a cylinder of base diameter 21 cm and length 18 cm fitted with conical ends each of axis length 9 cm. Determine the capacity of the tank.
If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket. (Use π = 22/7).
A solid piece of iron of dimensions 49 × 33 × 24 cm is moulded into a sphere. The radius of the sphere is
A hollow sphere of external and internal diameters 8 cm and 4 cm, respectively is melted into a solid cone of base diameter 8 cm. Find the height of the cone.
The volume of a right circular cylinder is 345 cm³. Then, the volume of a right circular cone whose radius of the base and height is the same as of circular cylinder will be ______.
A heap of rice is in the form of a cone of diameter 9 m and height 3.5 m. Find the volume of the rice. How much canvas cloth is required to just cover the heap?
A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm, 5 cm and 4 cm. The radius of each of the conical depressions is 0.5 cm and the depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand.
