Advertisements
Advertisements
प्रश्न
The cylinder of radius 12 cm have filled the 20 cm with water. One piece of iron drop in the stands of water goes up 6.75 cm. Find the radius of sphere piece.
उत्तर
Radius of cylinder = 12 cm
Height of cylinder = 6.75 cm
Volume of water = πr2h = π x 12 x 12 x 6.75 cm3
Let the radius of iron sphere piece = R cm.
∵ Volume of sphere = volume of water
`4/3` πR3 = π x 12 x 12 x 6.75
R3 = `(π xx 12 xx 12 xx 6.75 xx 3)/(4π)`
R3 = 729
R = `root(3)(729)` = 9 cm.
Hence radius of sphere piece = 9 cm.
APPEARS IN
संबंधित प्रश्न
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Find the surface area of a sphere of diameter 14 cm .
A spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made?
The volume of one sphere is 27 times that of another sphere. Calculate the ratio of their :
- radii,
- surface areas.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
Total volume of three identical cones is the same as that of a bigger cone whose height is 9 cm and diameter 40 cm. Find the radius of the base of each smaller cone, if height of each is 108 cm.
The total area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate :
- the radius of the solid sphere.
- the number of cones recast. [Take π = 3.14]
A hollow sphere of internal and external radii 6 cm and 8 cm respectively is melted and recast into small cones of base radius 2 cm and height 8 cm. Find the number of cones.
A solid is in the form of a cone standing on a hemi-sphere with both their radii being equal to 8 cm and the height of cone is equal to its radius. Find, in terms of π, the volume of the solid.
If a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.
The surface area of a sphere of radius 5 cm is five times the area of the curved surface of a cone of radius 4 cm. Find the height of the cone.
The total surface area of a hemisphere of radius r is
The largest sphere is cut off from a cube of side 6 cm. The volume of the sphere will be
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is
The ratio between the volume of a sphere and volume of a circumscribing right circular cylinder is
A cone and a hemisphere have equal bases and equal volumes the ratio of their heights is
Find the surface area of a sphere, if its volume is 38808 cubic cm. `(π = 22/7)`
A sphere has the same curved surface area as the curved surface area of a cone of height 36 cm and base radius 15 cm . Find the radius of the sphere .
The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm and the other dimensions are as shown.
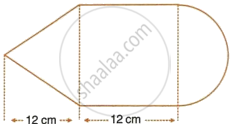
Calculate :
- the total surface area.
- the total volume of the solid and
- the density of the material if its total weight is 1.7 kg.
A vessel is in he form of an inverted cone. Its height is 11 cm., and the radius of its top which is open is 2.5 cm. It is filled with water up to the rim. When lead shots, each of which is a sphere of radius 0.25 cm., are dropped 2 into the vessel, `2/5`th of the water flows out. Find the number of lead shots dropped into the vessel.
